Advertisements
Advertisements
Question
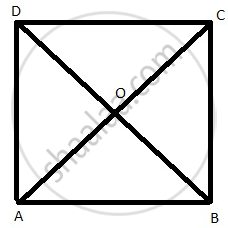
In a quadrilateral ABCD, AB = AD and CB = CD.
Prove that:
- AC bisects angle BAD.
- AC is the perpendicular bisector of BD.
Advertisements
Solution
Given: ABCD is quadrilateral,
AB = AD
CB = CD
To prove:
- AC bisects angle BAD.
- AC is the perpendicular bisector of BD.
Proof:
In ΔABC and ΔADC,
AB = AD ...(given)
CB = CD ...(given)
AC = AC ...(Common side)
ΔABC ≅ ΔADC ...(SSS)
∠BAD = ∠DAO ...(AC bisects A)
Therefore, AC bisects ∠BAD
OD = OB
OA = OC ...(diagonals bisect each other at O)
Thus, AC is perpendicular bisector of BD.
Hence, proved.
APPEARS IN
RELATED QUESTIONS
All rectangles are squares
Identify all the quadrilaterals that have four right angles
Explain how a square is a quadrilateral
Explain how a square is a rectangle
Prove that the bisectors of the interior angles of a rectangle form a square.
ABCD is a square. A is joined to a point P on BC and D is joined to a point Q on AB. If AP = DQ;
prove that AP and DQ are perpendicular to each other.
PQRS is a square whose diagonals PR and QS intersect at O.M is a point on QR such that OQ = MQ. Find the measures of ∠MOR and ∠QSR.
Prove that the quadrilateral formed by joining the mid-points of a square is also a square.
In the given figure, ΔPQR is right-angled at P. PABQ and QRST are squares on the side PQ and hypotenuse QR. If PN ⊥ TS, show that:
(a) ΔQRB ≅ ΔPQT
(b) Area of square PABQ = area of rectangle QTNM.
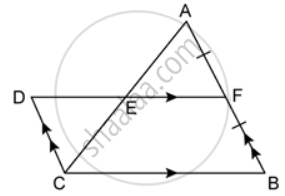
In a parallelogram PQRS, M and N are the midpoints of the sides PQ and PS respectively. If area of ΔPMN is 20 square units, find the area of the parallelogram PQRS.
