Advertisements
Chapters
2: Powers
3: Squares and Square Roots
4: Cubes and Cube Roots
5: Playing with Numbers
6: Algebraic Expressions and Identities
7: Factorization
8: Division of Algebraic Expressions
9: Linear Equation in One Variable
10: Direct and Inverse Variations
11: Time and Work
12: Percentage
13: Proft, Loss, Discount and Value Added Tax (VAT)
14: Compound Interest
15: Understanding Shapes-I (Polygons)
16: Understanding Shapes-II (Quadrilaterals)
▶ 17: Understanding Shapes-III (Special Types of Quadrilaterals)
18: Practical Geometry (Constructions)
19: Visualising Shapes
20: Mensuration - I (Area of a Trapezium and a Polygon)
21: Mensuration - II (Volumes and Surface Areas of a Cuboid and a Cube)
22: Mensuration - III (Surface Area and Volume of a Right Circular Cylinder)
23: Data Handling-I (Classification and Tabulation of Data)
24: Data Handling-II (Graphical Representation of Data as Histograms)
25: Data Handling-III (Pictorial Representation of Data as Pie Charts or Circle Graphs)
26: Data Handling-IV (Probability)
27: Introduction to Graphs
![RD Sharma solutions for Mathematics [English] Class 8 chapter 17 - Understanding Shapes-III (Special Types of Quadrilaterals) - Shaalaa.com](/images/9788189928049-mathematics-english-class-8_6:d71f9951bde04f9981d965449678818b.jpg "RD Sharma solutions for Mathematics [English] Class 8 chapter 17 - Understanding Shapes-III (Special Types of Quadrilaterals)")
Advertisements
Solutions for Chapter 17: Understanding Shapes-III (Special Types of Quadrilaterals)
Below listed, you can find solutions for Chapter 17 of CBSE RD Sharma for Mathematics [English] Class 8.
RD Sharma solutions for Mathematics [English] Class 8 17 Understanding Shapes-III (Special Types of Quadrilaterals) Exercise 17.1 [Pages 9 - 12]
Given below is a parallelogram ABCD. Complete each statement along with the definition or property used.
(i) AD =
(ii) ∠DCB =
(iii) OC =
(iv) ∠DAB + ∠CDA =
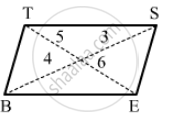
The following figure is parallelogram. Find the degree values of the unknowns x, y, z.
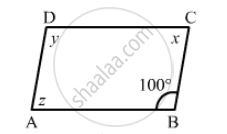
The following figure is parallelogram. Find the degree values of the unknown x, y, z.
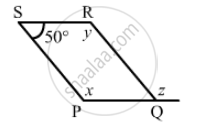
The following figure is parallelogram. Find the degree values of the unknown x, y, z.
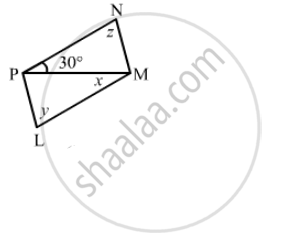
The following figure is parallelogram. Find the degree values of the unknown x, y, z.
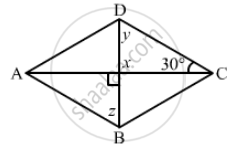
The following figure is parallelogram. Find the degree values of the unknown x, y, z.
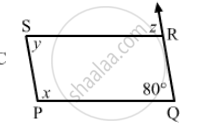
The following figure is parallelogram. Find the degree value of the unknown x, y, z.
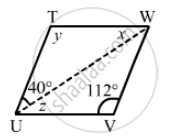
Can the following figure be parallelogram. Justify your answer.
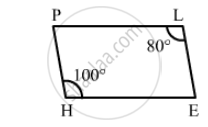
Can the following figure be parallelogram. Justify your answer.
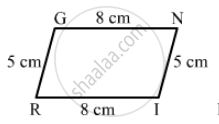
Can the following figure be parallelogram. Justify your answer.
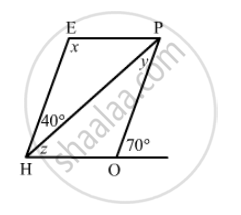
In the adjacent figure HOPE is a parallelogram. Find the angle measures x,y and z. State the geometrical truths you use to find them.
In the following figure GUNS and RUNS are parallelogram. Find x and y.
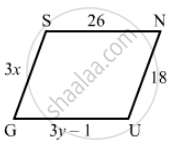
In the following figure GUNS and RUNS are parallelogram. Find x and y.
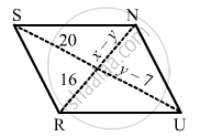
In the following figure RISK and CLUE are parallelograms. Find the measure of x.
Two opposite angles of a parallelogram are (3x − 2)° and (50 − x)°. Find the measure of each angle of the parallelogram.
If an angle of a parallelogram is two-third of its adjacent angle, find the angles of the parallelogram.
The measure of one angle of a parallelogram is 70°. What are the measures of the remaining angles?
Two adjacent angles of a parallelogram are as 1 : 2. Find the measures of all the angles of the parallelogram.
In a parallelogram ABCD, ∠D = 135°, determine the measure of ∠A and ∠B.
ABCD is a parallelogram in which ∠A = 70°. Compute ∠B, ∠C and ∠D.
The sum of two opposite angles of a parallelogram is 130°. Find all the angles of the parallelogram.
All the angles of a quadrilateral are equal to each other. Find the measure of each. Is the quadrilateral a parallelogram? What special type of parallelogram is it?
Two adjacent sides of a parallelogram are 4 cm and 3 cm respectively. Find its perimeter.
The perimeter of a parallelogram is 150 cm. One of its sides is greater than the other by 25 cm. Find the length of the sides of the parallelogram.
The shorter side of a parallelogram is 4.8 cm and the longer side is half as much again as the shorter side. Find the perimeter of the parallelogram.
Two adjacent angles of a parallelogram are (3x − 4)° and (3x + 10)°. Find the angles of the parallelogram.
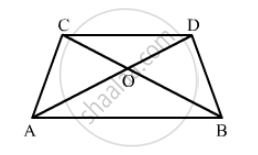
In a parallelogram ABCD, the diagonals bisect each other at O. If ∠ABC = 30°, ∠BDC = 10° and ∠CAB = 70°. Find:
∠DAB, ∠ADC, ∠BCD, ∠AOD, ∠DOC, ∠BOC, ∠AOB, ∠ACD, ∠CAB, ∠ADB, ∠ACB, ∠DBC and ∠DBA.
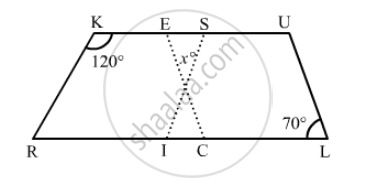
Find the angles marked with a question mark shown in Fig. 17.27
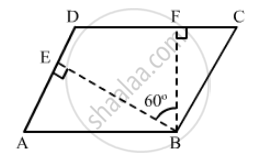
The angle between the altitudes of a parallelogram, through the same vertex of an obtuse angle of the parallelogram is 60°. Find the angles of the parallelogram.
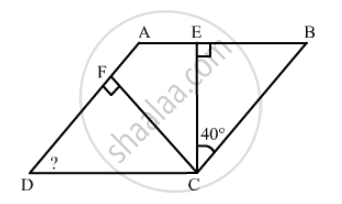
In the following figure, ABCD and AEFG are parallelograms. If ∠C = 55°, what is the measure of ∠F?
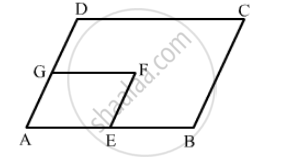
In the following figure, BDEF and DCEF are each a parallelogram. Is it true that BD = DC? Why or why not?
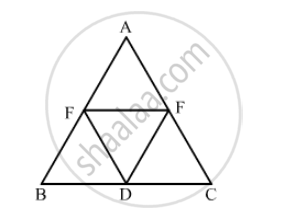
In Fig. 17.29, suppose it is known that DE = DF. Then, is ΔABC isosceles? Why or why not?
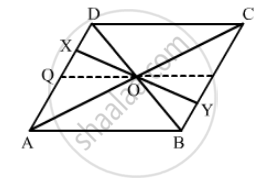
Diagonals of parallelogram ABCD intersect at O as shown in the following fegure. XY contains O, and X, Y are points on opposite sides of the parallelogram. Give reasons for each of the following:
(i) OB = OD
(ii) ∠OBY = ∠ODX
(iii) ∠BOY = ∠DOX
(iv) ∆BOY ≅ ∆DOX
Now, state if XY is bisected at O.
In the following Figure ABCD is a arallelogram, CE bisects ∠C and AF bisects ∠A. In each of the following, if the statement is true, give a reason for the same:
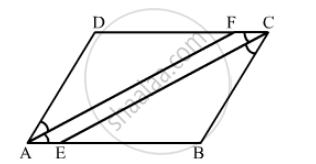
(i) ∠A = ∠C
(ii) \[\angle FAB = \frac{1}{2}\angle A\]
(iii) \[\angle DCE = \frac{1}{2}\angle C\]
(iv) \[\angle CEB = \angle FAB\]
(v) CE || AF
Diagonals of a parallelogram ABCD intersect at O. AL and CM are drawn perpendiculars to BD such that L and M lie on BD. Is AL = CM? Why or why not?
Points E and F lie on diagonal AC of a parallelogram ABCD such that AE = CF. What type of quadrilateral is BFDE?
In a parallelogram ABCD, AB = 10 cm, AD = 6 cm. The bisector of ∠A meets DC in E, AEand BC produced meet at F. Find te length CF.
RD Sharma solutions for Mathematics [English] Class 8 17 Understanding Shapes-III (Special Types of Quadrilaterals) Exercise 17.2 [Pages 16 - 17]
Which of the following statement is true for a rhombus?
It has two pairs of parallel sides.
Which of the following statement is true for a rhombus?
It has two pairs of equal sides.
Which of the following statement is true for a rhombus?
It has only two pairs of equal sides.
Which of the following statement is true for a rhombus?
Two of its angles are at right angles
Which of the following statement is true for a rhombus?
Its diagonals bisect each other at right angles.
Which of the following statement is true for a rhombus?
Its diagonals are equal and perpendicular.
Which of the following statement is true for a rhombus?
It has all its sides of equal lengths.
Which of the following statement is true for a rhombus?
It is a parallelogram.
Which of the following statement is true for a rhombus?
It is a quadrilateral.
Which of the following statement is true for a rhombus?
It can be a square.
Which of the following statement is true for a rhombus?
It is a square.
Fill in the blank, in the following, so as to make the statement true:
A rhombus is a parallelogram in which ......
Fill in the blank, inthe following, so as to make the statement true:
A square is a rhombus in which .....
Fill in the blank, inthe following, so as to make the statement true:
A rhombus has all its sides of ...... length.
Fill in the blank, in the following, so as to make the statement true:
The diagonals of a rhombus ...... each other at ...... angles.
Fill in the blank, in each of the following, so as to make the statement true:
If the diagonals of a parallelogram bisect each other at right angles, then it is a ......
The diagonals of a parallelogram are not perpendicular. Is it a rhombus? Why or why not?
The diagonals of a quadrilateral are perpendicular to each other. Is such a quadrilateral always a rhombus? If your answer is 'No', draw a figure to justify your answer.
ABCD is a rhombus. If ∠ACB = 40°, find ∠ADB.
If the diagonals of a rhombus are 12 cm and 16cm, find the length of each side.
Construct a rhombus whose diagonals are of length 10 cm and 6 cm.
Draw a rhombus, having each side of length 3.5 cm and one of the angles as 40°.
One side of a rhombus is of length 4 cm and the length of an altitude is 3.2 cm. Draw the rhombus.
Draw a rhombus ABCD, if AB = 6 cm and AC = 5 cm.
ABCD is a rhombus and its diagonals intersect at O.
(i) Is ∆BOC ≅ ∆DOC? State the congruence condition used?
(ii) Also state, if ∠BCO = ∠DCO.
Show that each diagonal of a rhombus bisects the angle through which it passes.
ABCD is a rhombus whose diagonals intersect at O. If AB = 10 cm, diagonal BD = 16 cm, find the length of diagonal AC.
The diagonals of a quadrilateral are of lengths 6 cm and 8 cm. If the diagonals bisect each other at right angles, what is the length of each side of the quadrilateral?
RD Sharma solutions for Mathematics [English] Class 8 17 Understanding Shapes-III (Special Types of Quadrilaterals) Exercise 17.3 [Pages 22 - 23]
Which of the following statement is true for a rectangle?
It has two pairs of equal sides.
Which of the following statement is true for a rectangle?
It has all its sides of equal length.
Which of the following statement is true for a rectangle?
Its diagonals are equal.
Which of the following statement is true for a rectangle?
Its diagonals bisect each other.
Which of the following statement is true for a rectangle?
Its diagonals are perpendicular.
Which of the following statement is true for a rectangle?
Its diagonals are perpendicular and bisect each other.
Which of the following statement is true for a rectangle?
Its diagonals are equal and bisect each other.
Which of the following statement is true for a rectangle?
Its diagonals are equal and perpendicular, and bisect each other.
Which of the following statement is true for a rectangle?
All rectangles are squares.
All rhombuses are parallelograms.
True
False
All squares are rhombuses and also rectangles.
True
False
All squares are not parallelograms.
True
False
Which of the following statement is true for a square?
It is a rectangle.
Which of the following statement are true for a square?
It has all its sides of equal length.
Which of the following statement true for a square?
Its diagonals bisect each other at right angle.
Which of the following statement true for a square?
Its diagonals are equal to its sides.
Fill in the blank in the following, so as to make the statement true:
A rectangle is a parallelogram in which .....
Fill in the blank in the following, so as to make the statement true:
A square is a rhombus in which .....
Fill in the blank of the following, so as to make the statement true:
A square is a rectangle in which .....
A window frame has one diagonal longer than the other. Is the window frame a rectangle? Why or why not?
In a rectangle ABCD, prove that ∆ACB ≅ ∆CAD.
The sides of a rectangle are in the ratio 2 : 3, and its perimeter is 20 cm. Draw the rectangle.
The sides of a rectangle are in the ratio 4 : 5. Find its sides if the perimeter is 90 cm.
Find the length of the diagonal of a rectangle whose sides are 12 cm and 5 cm.
Draw a rectangle whose one side measures 8 cm and the length of each of whose diagonals is 10 cm.
Draw a square whose each side measures 4.8 cm.
Identify all the quadrilateral that have Four sides of equal length
Identify all the quadrilaterals that have four right angles
Explain how a square is a quadrilateral
Explain how a square is a parallelogram
Explain how a square is a rhombus.
Explain how a square is a rectangle
Name the quadrilaterals whose diagonals bisect each other
Name the quadrilaterals whose diagonals are perpendicular bisectors of each other
Name the quadrilaterals whose diagonals are equal
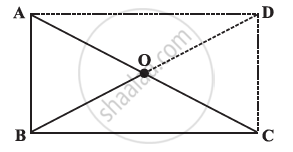
ABC is a right-angled triangle and O is the mid point of the side opposite to the right angle. Explain why O is equidistant from A, B and C. (The dotted lines are drawn additionally to help you)
A mason has made a concrete slab. He needs it to be rectangular. In what different ways can he make sure that it is rectangular?
Solutions for 17: Understanding Shapes-III (Special Types of Quadrilaterals)
RD Sharma solutions for Mathematics [English] Class 8 chapter 17 - Understanding Shapes-III (Special Types of Quadrilaterals)
Shaalaa.com has the CBSE Mathematics Mathematics [English] Class 8 CBSE solutions in a manner that help students grasp basic concepts better and faster. The detailed, step-by-step solutions will help you understand the concepts better and clarify any confusion. RD Sharma solutions for Mathematics Mathematics [English] Class 8 CBSE 17 (Understanding Shapes-III (Special Types of Quadrilaterals)) include all questions with answers and detailed explanations. This will clear students' doubts about questions and improve their application skills while preparing for board exams.
Further, we at Shaalaa.com provide such solutions so students can prepare for written exams. RD Sharma textbook solutions can be a core help for self-study and provide excellent self-help guidance for students.
Concepts covered in Mathematics [English] Class 8 chapter 17 Understanding Shapes-III (Special Types of Quadrilaterals) are Properties of Trapezium, Properties of Kite, Classification of Polygons, Properties of a Parallelogram, Concept of Curves, Interior Angles of a Polygon, Exterior Angles of a Polygon and Its Property, Concept of Polygons, Concept of Quadrilaterals, Property: The diagonals of a rhombus are perpendicular bisectors of one another., Properties of Rhombus, Property: The Opposite Sides of a Parallelogram Are of Equal Length., Property: The Opposite Angles of a Parallelogram Are of Equal Measure., Property: The adjacent angles in a parallelogram are supplementary., Property: The diagonals of a parallelogram bisect each other. (at the point of their intersection), Property: The Diagonals of a Rectangle Are of Equal Length., Properties of Rectangle, Properties of a Square, Property: The diagonals of a square are perpendicular bisectors of each other., Properties of a Quadrilateral, Different Types of Curves - Closed Curve, Open Curve, Simple Curve..
Using RD Sharma Mathematics [English] Class 8 solutions Understanding Shapes-III (Special Types of Quadrilaterals) exercise by students is an easy way to prepare for the exams, as they involve solutions arranged chapter-wise and also page-wise. The questions involved in RD Sharma Solutions are essential questions that can be asked in the final exam. Maximum CBSE Mathematics [English] Class 8 students prefer RD Sharma Textbook Solutions to score more in exams.
Get the free view of Chapter 17, Understanding Shapes-III (Special Types of Quadrilaterals) Mathematics [English] Class 8 additional questions for Mathematics Mathematics [English] Class 8 CBSE, and you can use Shaalaa.com to keep it handy for your exam preparation.
