Advertisements
Advertisements
Question
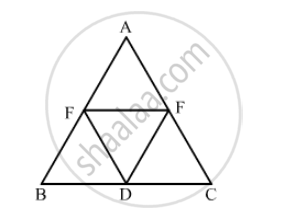
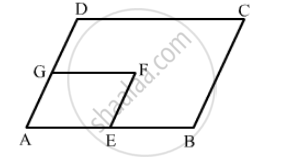
In the following figure, BDEF and DCEF are each a parallelogram. Is it true that BD = DC? Why or why not?
Solution
\[\text{ In parallelogram BDEF }\]
\[ \therefore BD = EF . . . (i) (\text{ opposite sides of a parallelogram are equal })\]
\[\text{ In parallelogram DCEF }\]
\[ CD = EF . . . (ii) (\text{ opposite sides of a parallelogram are equal })\]
\[\text{ From equations (i) and } (ii)\]
\[BD = CD\]
APPEARS IN
RELATED QUESTIONS
In the following figure, ABCD and AEFG are parallelograms. If ∠C = 55°, what is the measure of ∠F?
In Fig. 17.29, suppose it is known that DE = DF. Then, is ΔABC isosceles? Why or why not?
Which of the following statement true for a square?
Its diagonals are equal to its sides.
In a rectangle ABCD, prove that ∆ACB ≅ ∆CAD.
Using opposite angles test for parallelogram, prove that every rectangle is a parallelogram.
Diagonals of a rectangle ABCD intersect at point O. If AC = 8 cm then find BO and if ∠CAD =35° then find ∠ACB.
State with Reason Whether the Following Statement is ‘True’ Or ‘False’.
Every rectangle is a parallelogram.
Rectangle is a regular quadrilateral.
If diagonals of a quadrilateral are equal, it must be a rectangle.
Every parallelogram is a rectangle.
