Advertisements
Advertisements
Question
In the following figure, ABCD and AEFG are parallelograms. If ∠C = 55°, what is the measure of ∠F?
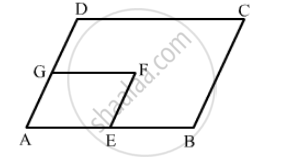
Solution
\[\text{ Both the parallelograms ABCD and AEFG are similar } . \]
\[ \therefore \angle C = \angle A = 55° (\text{ opposite angles of a parallelogram are equal })\]
\[ \therefore \angle A = \angle F = 55° (\text{ opposite angles of a parallelogram are equal })\]
APPEARS IN
RELATED QUESTIONS
Which of the following statement is true for a rectangle?
It has all its sides of equal length.
Which of the following statement true for a square?
Its diagonals are equal to its sides.
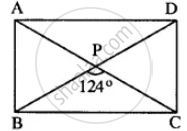
ABCD is a rectangle, if ∠BPC = 124°
Calculate:
- ∠BAP
- ∠ADP
The interior angle made by the side in a parallelogram is 90° then the parallelogram is a
If the diagonals of a quadrilateral are equal and bisect each other, then the quadrilateral is a ______.
Every parallelogram is a rectangle.
Every trapezium is a rectangle.
In a rectangle ABCD, AB = 25 cm and BC = 15. In what ratio does the bisector of ∠C divide AB?
PQRS is a rectangle. The perpendicular ST from S on PR divides ∠S in the ratio 2:3. Find ∠TPQ.
A line l is parallel to line m and a transversal p intersects them at X, Y respectively. Bisectors of interior angles at X and Y interesct at P and Q. Is PXQY a rectangle? Given reason.
