Advertisements
Advertisements
Question
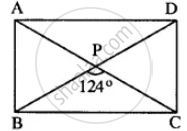
ABCD is a rectangle, if ∠BPC = 124°
Calculate:
- ∠BAP
- ∠ADP
Solution
Given:
- Rectangle ABCD
- ∠BPC = 124∘
Key Properties of a Rectangle:
- Diagonals of a rectangle bisect each other.
- Opposite angles formed by the diagonals are equal (angles around point P add up to 360∘).
Calculate ∠BAP:
-
In △ABP, diagonal AC divides ∠BAP and ∠BPC.
-
Since diagonals of a rectangle bisect each other, the total angles around point P are split symmetrically.
- Opposite angles: ∠BPC + ∠DPA = 180∘
Hence, ∠DPA = 180∘ − 124∘ = 56∘
Now, ∠BAP = `(∠DPA)/2`
`∠BAP = (56°)/2 = 28°`
Calculate ∠ADP:
Similarly, ∠ADP is the other half of ∠DPA:
`∠ADP = (∠DPA)/2 = 28°`
Final Answers:
- ∠BAP = 28∘
- ∠ADP = 28∘
APPEARS IN
RELATED QUESTIONS
In a parallelogram ABCD, the diagonals bisect each other at O. If ∠ABC = 30°, ∠BDC = 10° and ∠CAB = 70°. Find:
∠DAB, ∠ADC, ∠BCD, ∠AOD, ∠DOC, ∠BOC, ∠AOB, ∠ACD, ∠CAB, ∠ADB, ∠ACB, ∠DBC and ∠DBA.
Which of the following statement is true for a rectangle?
Its diagonals are equal.
Which of the following statement is true for a rectangle?
Its diagonals are equal and perpendicular, and bisect each other.
Which of the following statement are true for a square?
It has all its sides of equal length.
Which of the following statement true for a square?
Its diagonals bisect each other at right angle.
Draw a rectangle whose one side measures 8 cm and the length of each of whose diagonals is 10 cm.
Draw a square whose each side measures 4.8 cm.
Prove that quadrilateral formed by the intersection of angle bisectors of all angles of a parallelogram is a rectangle.
A parallelogram PQRS is constructed with sides QR = 6 cm, PQ = 4 cm and ∠PQR = 90°. Then PQRS is a ______.
All squares are rectangles.
