Advertisements
Advertisements
Question
In a parallelogram ABCD, the diagonals bisect each other at O. If ∠ABC = 30°, ∠BDC = 10° and ∠CAB = 70°. Find:
∠DAB, ∠ADC, ∠BCD, ∠AOD, ∠DOC, ∠BOC, ∠AOB, ∠ACD, ∠CAB, ∠ADB, ∠ACB, ∠DBC and ∠DBA.
Solution
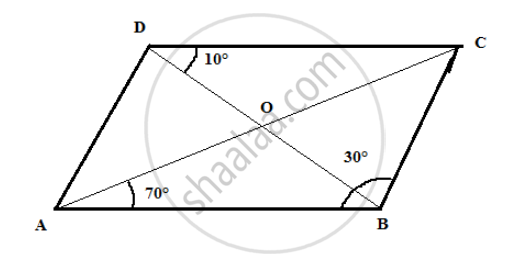
\[\angle ABC = 30°\]
\[ \therefore \angle ADC = 30° \left( \text{ opposite angle of the parallelogram }\right)\]
\[\text{ and } \angle BDA = \angle ADC - \angle BDC = 30° - 10° = 20°\]
\[\angle BAC = \angle ACD = 70°(\text{ alternate angle })\]
\[\text{ In } \bigtriangleup ABC: \]
\[\angle CAB + \angle ABC + \angle BCA = 180°\]
\[70° + 30° + \angle BCA = 180°\]
\[ \therefore \angle BCA = 80°\]
\[\angle DAB = \angle DAC + \angle CAB = 70° + 80°= 150°\]
\[\angle BCD = 150° \left( \text{ opposite angle of the parallelogram } \right)\]
\[\angle DCA = \angle CAB = 70°\]
\[\text{ In } \bigtriangleup DOC: \]
\[\angle ODC + \angle DOC + \angle OCD = 180\]
\[10° + 70°+ \angle DOC = 180°\]
\[ \therefore \angle DOC = 100°\]
\[\angle DOC + \angle BOC = 180°\]
\[\angle BOC = 180° - 100°\]
\[\angle BOC = 80°\]
\[\angle AOD = \angle BOC = 80° \left( \text{ vertically opposite angles } \right) \]
\[\angle AOB = \angle DOC = 100° \left( \text{ vertically opposite angles } \right) \]
\[\angle CAB = 70° \left( \text{ given } \right)\]
\[\angle ADB = 20°\]
\[\angle DBA = \angle BDC = 10°(\text{ alternate angle })\]
\[\angle ADB = \angle DBC = 20°(\text{ alternate angle })\]
APPEARS IN
RELATED QUESTIONS
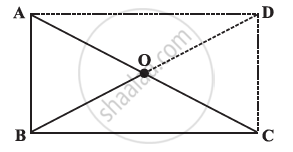
ABC is a right-angled triangle and O is the mid point of the side opposite to the right angle. Explain why O is equidistant from A, B and C. (The dotted lines are drawn additionally to help you)
Which of the following statement is true for a rectangle?
Its diagonals bisect each other.
Which of the following statement is true for a square?
It is a rectangle.
Fill in the blank in the following, so as to make the statement true:
A rectangle is a parallelogram in which .....
A window frame has one diagonal longer than the other. Is the window frame a rectangle? Why or why not?
Using opposite angles test for parallelogram, prove that every rectangle is a parallelogram.
Draw a rectangle ABCD such that l(AB) = 6.0 cm and l (BC) = 4.5 cm.
The interior angle made by the side in a parallelogram is 90° then the parallelogram is a
If diagonals of a quadrilateral are equal, it must be a rectangle.
A rectangular MORE is shown below:
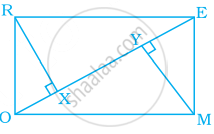
Answer the following questions by giving appropriate reason.
- Is RE = OM?
- Is ∠MYO = ∠RXE?
- Is ∠MOY = ∠REX?
- Is ΔMYO ≅ ΔRXE?
- Is MY = RX?
