Advertisements
Advertisements
Question
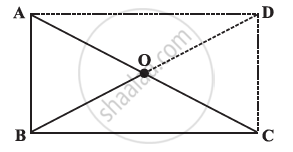
ABC is a right-angled triangle and O is the mid point of the side opposite to the right angle. Explain why O is equidistant from A, B and C. (The dotted lines are drawn additionally to help you)
Solution
ABCD is a rectangle as opposite sides are equal and parallel to each other, and all the interior angles are 90º.
In a rectangle, diagonals are of equal length and also these bisect each other.
Since MBC is right-angled at B. So ∠D = 90°, AD||BC and AB||DC
ABCD is a rectangle where AB = CD and AD=BC
AC and BD are the diagonals which bisect each other.
Hence, AO = OC = BO = OD
Thus, O is equidistant from A, B, and C.
APPEARS IN
RELATED QUESTIONS
Name the quadrilaterals whose diagonals are equal
In a parallelogram ABCD, the diagonals bisect each other at O. If ∠ABC = 30°, ∠BDC = 10° and ∠CAB = 70°. Find:
∠DAB, ∠ADC, ∠BCD, ∠AOD, ∠DOC, ∠BOC, ∠AOB, ∠ACD, ∠CAB, ∠ADB, ∠ACB, ∠DBC and ∠DBA.
Fill in the blank of the following, so as to make the statement true:
A square is a rectangle in which .....
In a rectangle ABCD, prove that ∆ACB ≅ ∆CAD.
Find the length of the diagonal of a rectangle whose sides are 12 cm and 5 cm.
Draw a rectangle ABCD such that l(AB) = 6.0 cm and l (BC) = 4.5 cm.
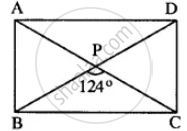
ABCD is a rectangle, if ∠BPC = 124°
Calculate:
- ∠BAP
- ∠ADP
A parallelogram PQRS is constructed with sides QR = 6 cm, PQ = 4 cm and ∠PQR = 90°. Then PQRS is a ______.
All squares are rectangles.
PQRS is a rectangle. The perpendicular ST from S on PR divides ∠S in the ratio 2:3. Find ∠TPQ.
