Advertisements
Advertisements
Question
PQRS is a rectangle. The perpendicular ST from S on PR divides ∠S in the ratio 2:3. Find ∠TPQ.
Solution
Given, ST ⊥ PR and ST divides ∠S in the ratio 2:3
So, sum of ratio = 2 + 3 = 5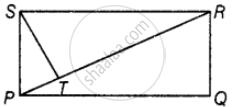
Now, `∠TSP = 2/5 xx 90^circ = 36^circ, ∠TSR = 3/5 xx 90^circ = 54^circ`
Also, by the angle sum property of a triangle,
∠TPS = 180° – (∠STP + ∠TSP)
= 180° – (90° + 36°)
= 54°
We know that, ∠SPQ = 90°
⇒ ∠TPS + ∠TPQ = 90°
⇒ 54° + ∠TPQ = 90°
⇒ ∠TPQ = 90° – 54° = 36°
APPEARS IN
RELATED QUESTIONS
In the following figure, BDEF and DCEF are each a parallelogram. Is it true that BD = DC? Why or why not?
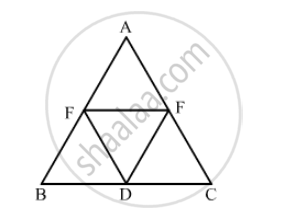
In Fig. 17.29, suppose it is known that DE = DF. Then, is ΔABC isosceles? Why or why not?
Diagonals of a parallelogram ABCD intersect at O. AL and CM are drawn perpendiculars to BD such that L and M lie on BD. Is AL = CM? Why or why not?
Which of the following statement are true for a square?
It has all its sides of equal length.
In a rectangle ABCD, prove that ∆ACB ≅ ∆CAD.
Using opposite angles test for parallelogram, prove that every rectangle is a parallelogram.
State with Reason Whether the Following Statement is ‘True’ Or ‘False’.
Every rectangle is a parallelogram.
For which of the following figures, diagonals are equal?
All squares are rectangles.
In a rectangle ABCD, AB = 25 cm and BC = 15. In what ratio does the bisector of ∠C divide AB?
