Advertisements
Advertisements
Question
Diagonals of a parallelogram ABCD intersect at O. AL and CM are drawn perpendiculars to BD such that L and M lie on BD. Is AL = CM? Why or why not?
Solution

\[\text{ In } \Delta AOL \text{ and } \Delta CMO: \]
\[\angle AOL = \angle COM( \text{ vertically opposite angle }) . . . . (i)\]
\[\angle ALO = \angle CMO = 90° (\text{ each right angle }) . . . . . (ii)\]
\[\text{ Using angle sum property }: \]
\[\angle AOL + \angle ALO + \angle LAO = 180° . . . . . . . . . . (iii)\]
\[\angle COM + \angle CMO + \angle OCM = 180°. . . . . . (iv)\]
\[\text{ From equations } (iii) \text{ and } (iv): \]
\[\angle AOL + \angle ALO + \angle LAO = \angle COM + \angle CMO + \angle OCM\]
\[\angle LAO = \angle OCM (\text{ from equations (i) and } (ii) )\]
\[In \Delta AOL \text{ and }\Delta CMO: \]
\[\angle ALO = \angle CMO (\text{ each right angle })\]
\[AO = OC (\text{ diagonals of a parallelogram bisect each other })\]
\[\angle LAO = \angle OCM (\text{ proved above })\]
\[\text{ So }, \Delta AOL \text{ is congruent to } \Delta CMO (SAS) . \]
\[ \Rightarrow AL = CM [cpct]\]
APPEARS IN
RELATED QUESTIONS
The shorter side of a parallelogram is 4.8 cm and the longer side is half as much again as the shorter side. Find the perimeter of the parallelogram.
In the following figure, ABCD and AEFG are parallelograms. If ∠C = 55°, what is the measure of ∠F?
Which of the following statement is true for a rectangle?
Its diagonals bisect each other.
Which of the following statement is true for a rectangle?
Its diagonals are perpendicular.
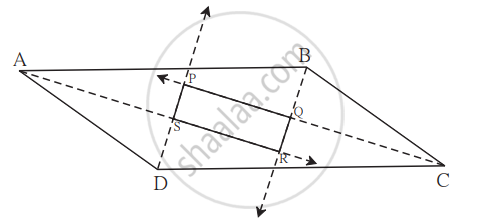
Prove that quadrilateral formed by the intersection of angle bisectors of all angles of a parallelogram is a rectangle.
ABCD is a rectangle whose diagonals AC and BD intersect at O. If ∠OAB = 46°, find ∠OBC
Show that the bisectors of angles of a parallelogram form a rectangle
For which of the following figures, diagonals are equal?
A quadrilateral whose opposite sides and all the angles are equal is a ______.
If the adjacent angles of a parallelogram are equal, then the parallelogram is a ______.
