Advertisements
Advertisements
Question
A quadrilateral whose opposite sides and all the angles are equal is a ______.
Options
rectangle
parallelogram
square
rhombus
Solution
A quadrilateral whose opposite sides and all the angles are equal is a rectangle.
Explanation:
We know that, in a rectangle, opposite sides and all the angles are equal.
APPEARS IN
RELATED QUESTIONS
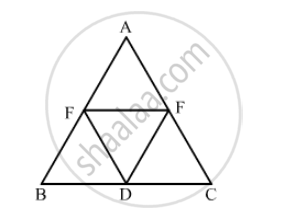
In the following figure, BDEF and DCEF are each a parallelogram. Is it true that BD = DC? Why or why not?
Diagonals of a parallelogram ABCD intersect at O. AL and CM are drawn perpendiculars to BD such that L and M lie on BD. Is AL = CM? Why or why not?
Which of the following statement is true for a square?
It is a rectangle.
Which of the following statement are true for a square?
It has all its sides of equal length.
In a rectangle ABCD, prove that ∆ACB ≅ ∆CAD.
The sides of a rectangle are in the ratio 2 : 3, and its perimeter is 20 cm. Draw the rectangle.
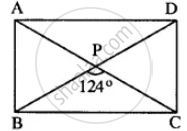
ABCD is a rectangle, if ∠BPC = 124°
Calculate:
- ∠BAP
- ∠ADP
Show that the bisectors of angles of a parallelogram form a rectangle
If diagonals of a quadrilateral are equal, it must be a rectangle.
A rectangular MORE is shown below:
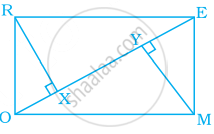
Answer the following questions by giving appropriate reason.
- Is RE = OM?
- Is ∠MYO = ∠RXE?
- Is ∠MOY = ∠REX?
- Is ΔMYO ≅ ΔRXE?
- Is MY = RX?
