Advertisements
Advertisements
Question
In a rectangle ABCD, prove that ∆ACB ≅ ∆CAD.
Solution
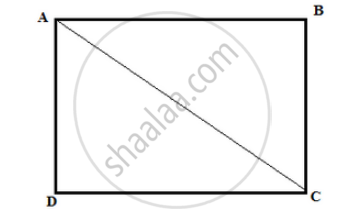
In ∆ACB and ∆CAD:
AB = CD (rectangle property)
AD = BC (rectangle property)
AC ( common side )
Hence, by SSS criterion, it is proved that\[∆ ACB \cong ∆ CAD\]
APPEARS IN
RELATED QUESTIONS
Diagonals of a parallelogram ABCD intersect at O. AL and CM are drawn perpendiculars to BD such that L and M lie on BD. Is AL = CM? Why or why not?
Which of the following statement is true for a rectangle?
It has all its sides of equal length.
Which of the following statement is true for a rectangle?
All rectangles are squares.
A window frame has one diagonal longer than the other. Is the window frame a rectangle? Why or why not?
Diagonals of a rectangle ABCD intersect at point O. If AC = 8 cm then find BO and if ∠CAD =35° then find ∠ACB.
Adjacent sides of a rectangle are 7 cm and 24 cm. Find the length of its diagonal.
ABCD is a rectangle whose diagonals AC and BD intersect at O. If ∠OAB = 46°, find ∠OBC
For which of the following figures, diagonals are equal?
A quadrilateral whose opposite sides and all the angles are equal is a ______.
Construct a rectangle whose one side is 3 cm and a diagonal equal to 5 cm.
