Advertisements
Advertisements
प्रश्न
In a rectangle ABCD, prove that ∆ACB ≅ ∆CAD.
उत्तर
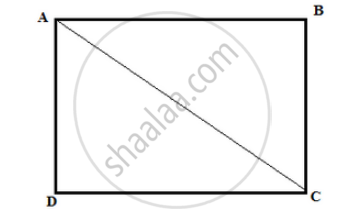
In ∆ACB and ∆CAD:
AB = CD (rectangle property)
AD = BC (rectangle property)
AC ( common side )
Hence, by SSS criterion, it is proved that\[∆ ACB \cong ∆ CAD\]
APPEARS IN
संबंधित प्रश्न
Which of the following statement is true for a rectangle?
Its diagonals are perpendicular.
Which of the following statement is true for a rectangle?
Its diagonals are equal and perpendicular, and bisect each other.
Fill in the blank of the following, so as to make the statement true:
A square is a rectangle in which .....
A window frame has one diagonal longer than the other. Is the window frame a rectangle? Why or why not?
Diagonals of a rectangle ABCD intersect at point O. If AC = 8 cm then find BO and if ∠CAD =35° then find ∠ACB.
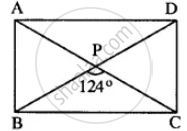
ABCD is a rectangle, if ∠BPC = 124°
Calculate:
- ∠BAP
- ∠ADP
For which of the following figures, all angles are equal?
If the adjacent angles of a parallelogram are equal, then the parallelogram is a ______.
Every parallelogram is a rectangle.
In a rectangle ABCD, AB = 25 cm and BC = 15. In what ratio does the bisector of ∠C divide AB?
