Advertisements
Advertisements
प्रश्न
In a rectangle ABCD, prove that ∆ACB ≅ ∆CAD.
उत्तर
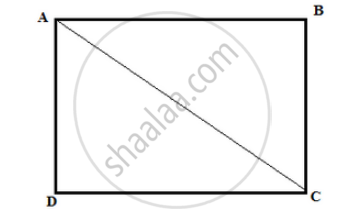
In ∆ACB and ∆CAD:
AB = CD (rectangle property)
AD = BC (rectangle property)
AC ( common side )
Hence, by SSS criterion, it is proved that\[∆ ACB \cong ∆ CAD\]
APPEARS IN
संबंधित प्रश्न
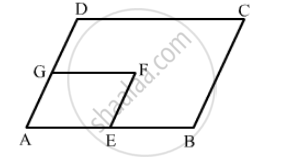
In the following figure, ABCD and AEFG are parallelograms. If ∠C = 55°, what is the measure of ∠F?
Which of the following statement true for a square?
Its diagonals are equal to its sides.
Fill in the blank of the following, so as to make the statement true:
A square is a rectangle in which .....
A mason has made a concrete slab. He needs it to be rectangular. In what different ways can he make sure that it is rectangular?
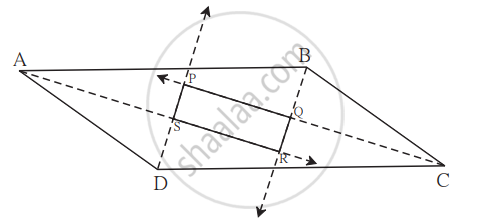
Prove that quadrilateral formed by the intersection of angle bisectors of all angles of a parallelogram is a rectangle.
If diagonal of a rectangle is 26 cm and one side is 24 cm, find the other side.
If the diagonals of a parallelogram are of equal lengths, the parallelogram is a rectangle. Prove it.
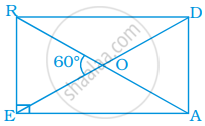
ABCD is a rectangle whose diagonals AC and BD intersect at O. If ∠OAB = 46°, find ∠OBC
A parallelogram PQRS is constructed with sides QR = 6 cm, PQ = 4 cm and ∠PQR = 90°. Then PQRS is a ______.
In rectangle READ, find ∠EAR, ∠RAD and ∠ROD