Advertisements
Advertisements
प्रश्न
If the diagonals of a parallelogram are of equal lengths, the parallelogram is a rectangle. Prove it.
उत्तर
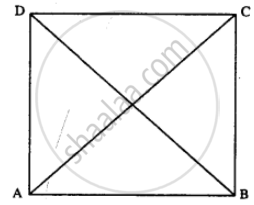
Given : //gm ABCD in which AC = BD
To Prove: ABCD is rectangle.
Proof : In ∆ABC and ∆ABD
AB = AB (Common)
AC = BD (Given)
BC = AD (opposite sides of ||gm)
∆ABC = ∆ABD (S.S.S. Rule)
∠A = ∠B
But AD // BC (opp. sides of ||gm are ||)
∠A + ∠B = 180°
∠A = ∠B = 90°
Similarly ∠D = ∠C = 90°
Hence ABCD is a rectangle.
APPEARS IN
संबंधित प्रश्न
Name the quadrilaterals whose diagonals are equal
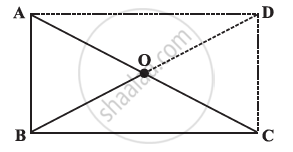
ABC is a right-angled triangle and O is the mid point of the side opposite to the right angle. Explain why O is equidistant from A, B and C. (The dotted lines are drawn additionally to help you)
In Fig. 17.29, suppose it is known that DE = DF. Then, is ΔABC isosceles? Why or why not?
Diagonals of a parallelogram ABCD intersect at O. AL and CM are drawn perpendiculars to BD such that L and M lie on BD. Is AL = CM? Why or why not?
Which of the following statement is true for a rectangle?
All rectangles are squares.
The sides of a rectangle are in the ratio 4 : 5. Find its sides if the perimeter is 90 cm.
Using opposite angles test for parallelogram, prove that every rectangle is a parallelogram.
State with Reason Whether the Following Statement is ‘True’ Or ‘False’.
Every rectangle is a parallelogram.
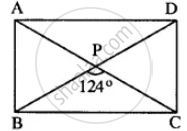
ABCD is a rectangle, if ∠BPC = 124°
Calculate:
- ∠BAP
- ∠ADP
A line l is parallel to line m and a transversal p intersects them at X, Y respectively. Bisectors of interior angles at X and Y interesct at P and Q. Is PXQY a rectangle? Given reason.
