Advertisements
Advertisements
प्रश्न
In parallelogram ABCD, E is the mid-point of AD and F is the mid-point of BC. Prove that BFDE is a parallelogram.
उत्तर
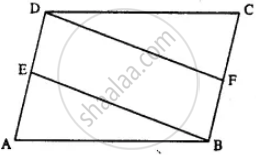
Given: Parallelogram ABCD in which E and F are mid-points of AD and BC respectively.
To Prove: BFDE is a Parallelogram.
Proof: E is the mid-point of AD. (Given)
DE = `1/2` AD
Also, F is mid-point of BC (Given)
BF = `1/2` BC
But AD = BC (opp. sides of parallelogram)
BF = DE
Again AD || BC
⇒ DE || BF
Now DE || BF and DE = BF
Hence BFDE is a parallelogram.
APPEARS IN
संबंधित प्रश्न
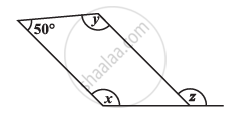
Consider the given parallelogram. Find the values of the unknowns x, y, z.
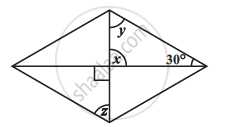
Consider the given parallelograms. Find the values of the unknowns x, y, z.
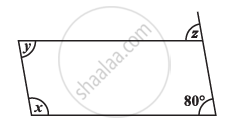
Consider the given parallelograms. Find the values of the unknowns x, y, z.
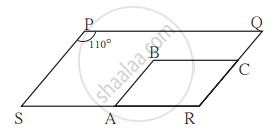
In the given figure, `square`PQRS and `square`ABCR are two parallelograms. If ∠P = 110° then find the measures of all angles of `square`ABCR.
Construct a parallelogram ABCD such that l(BC) = 7 cm, m∠ABC = 40° , l(AB) = 3 cm.
Prove that the diagonals of a parallelogram bisect each other.
The given figure shows parallelogram ABCD. Points M and N lie in diagonal BD such that DM = BN.
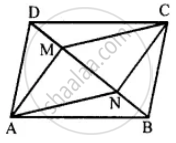
Prove that:
(i) ∆DMC = ∆BNA and so CM = AN
(ii) ∆AMD = ∆CNB and so AM CN
(iii) ANCM is a parallelogram.
In parallelogram MODE, the bisector of ∠M and ∠O meet at Q, find the measure of ∠MQO.
ABCD is a parallelogram. Find the value of x, y and z.

ABCD is a parallelogram. The bisector of angle A intersects CD at X and bisector of angle C intersects AB at Y. Is AXCY a parallelogram? Give reason.
