Advertisements
Advertisements
Question
In parallelogram ABCD, E is the mid-point of AD and F is the mid-point of BC. Prove that BFDE is a parallelogram.
Solution
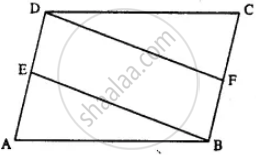
Given: Parallelogram ABCD in which E and F are mid-points of AD and BC respectively.
To Prove: BFDE is a Parallelogram.
Proof: E is the mid-point of AD. (Given)
DE = `1/2` AD
Also, F is mid-point of BC (Given)
BF = `1/2` BC
But AD = BC (opp. sides of parallelogram)
BF = DE
Again AD || BC
⇒ DE || BF
Now DE || BF and DE = BF
Hence BFDE is a parallelogram.
APPEARS IN
RELATED QUESTIONS
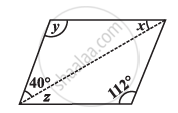
Consider the given parallelograms. Find the values of the unknowns x, y, z.
Can a quadrilateral ABCD be a parallelogram if ∠D + ∠B = 180°?
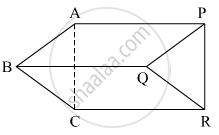
In the adjacent figure, if seg AB || seg PQ, seg AB ≅ seg PQ, seg AC || seg PR, seg AC ≅ seg PR then prove that, seg BC || seg QR and seg BC ≅ seg QR.
Construct ☐ BARC such that l(BA) = l(BC) = 4.2 cm, l(AC) = 6.0 cm, l(AR) = l(CR) = 5.6 cm
ABCD is a parallelogram. What kind of quadrilateral is it if : AC = BD and AC is perpendicular to BD?
Prove that the diagonals of a parallelogram bisect each other.
In parallelogram ABCD, E is the mid-point of side AB and CE bisects angle BCD. Prove that :
(i) AE = AD,
(ii) DE bisects and ∠ADC and
(iii) Angle DEC is a right angle.
The given figure shows parallelogram ABCD. Points M and N lie in diagonal BD such that DM = BN.
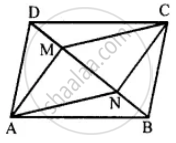
Prove that:
(i) ∆DMC = ∆BNA and so CM = AN
(ii) ∆AMD = ∆CNB and so AM CN
(iii) ANCM is a parallelogram.
A diagonal of a parallelogram bisects an angle. Will it also bisect the other angle? Give reason.
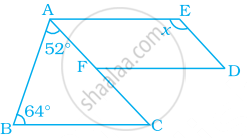
In the following figure, FD || BC || AE and AC || ED. Find the value of x.