Advertisements
Advertisements
Question
In the following figure, FD || BC || AE and AC || ED. Find the value of x.
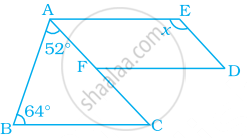
Solution
Given: FD || BC || AE and AC || ED.
Construction: Produce DF such that it intersect AB at G.
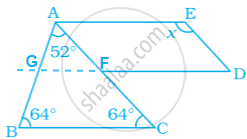
In triangle ABC,
∠A + ∠B + ∠C = 180° ...[Angle sum property of triangle]
52° + 64° + ∠C = 180°
∠C = 180° – (52° + 64°)
∠C = 180° – 116°
∠C = 64°
Now, as see that DG || BC and DG || AE,
∠ACB = ∠AFG ...[FG || BC and FC is a transversal. So, corresponding angles]
64° = ∠AFG
Also, GFD is a straight line.
So, ∠GFA + ∠AFD = 180° ...[Linear pair]
64° + ∠AFD = 180°
∠AFD = 180° – 64°
∠AFD = 116°
Also, FD || AE and AF || ED
Hence, AEDF is a parallelogram.
Now, ∠AFD = ∠AEF ...[Opposite angles in a parallelogram are equal]
∠AED = x = 116°
APPEARS IN
RELATED QUESTIONS
If the ratio of measures of two adjacent angles of a parallelogram is 1 : 2, find the measures of all angles of the parallelogram.
In parallelogram ABCD, ∠A = 3 times ∠B. Find all the angles of the parallelogram. In the same parallelogram, if AB = 5x – 7 and CD = 3x +1 ; find the length of CD.
ABCD is a parallelogram. What kind of quadrilateral is it if: AC is perpendicular to BD but is not equal to it?
In parallelogram ABCD, E is the mid-point of side AB and CE bisects angle BCD. Prove that :
(i) AE = AD,
(ii) DE bisects and ∠ADC and
(iii) Angle DEC is a right angle.
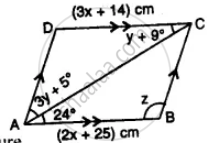
Use the information given in the alongside diagram to find the value of x, y, and z.
Which of the following figures satisfy the following properties?
- All sides are congruent.
- All angles are right angles.
- Opposite sides are parallel.
If two adjacent angles of a parallelogram are (5x – 5)° and (10x + 35)°, then the ratio of these angles is ______.
In the given figure, ABCD and BDCE are parallelograms with common base DC. If BC ⊥ BD, then ∠BEC = ______.

In parallelogram MODE, the bisector of ∠M and ∠O meet at Q, find the measure of ∠MQO.
The angle between the two altitudes of a parallelogram through the vertex of an obtuse angle of the parallelogram is 45°. Find the angles of the parallelogram.
