Advertisements
Advertisements
प्रश्न
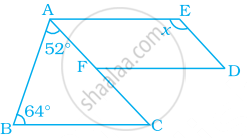
In the following figure, FD || BC || AE and AC || ED. Find the value of x.
उत्तर
Given: FD || BC || AE and AC || ED.
Construction: Produce DF such that it intersect AB at G.
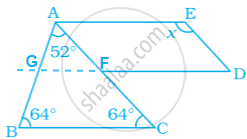
In triangle ABC,
∠A + ∠B + ∠C = 180° ...[Angle sum property of triangle]
52° + 64° + ∠C = 180°
∠C = 180° – (52° + 64°)
∠C = 180° – 116°
∠C = 64°
Now, as see that DG || BC and DG || AE,
∠ACB = ∠AFG ...[FG || BC and FC is a transversal. So, corresponding angles]
64° = ∠AFG
Also, GFD is a straight line.
So, ∠GFA + ∠AFD = 180° ...[Linear pair]
64° + ∠AFD = 180°
∠AFD = 180° – 64°
∠AFD = 116°
Also, FD || AE and AF || ED
Hence, AEDF is a parallelogram.
Now, ∠AFD = ∠AEF ...[Opposite angles in a parallelogram are equal]
∠AED = x = 116°
APPEARS IN
संबंधित प्रश्न
Can a quadrilateral ABCD be a parallelogram if ∠A = 70° and ∠C = 65°?
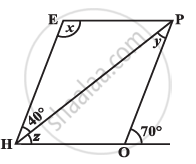
The adjacent figure HOPE is a parallelogram. Find the angle measures x, y and z. State the properties you use to find them.
Construct ☐ BARC such that l(BA) = l(BC) = 4.2 cm, l(AC) = 6.0 cm, l(AR) = l(CR) = 5.6 cm
Construct a parallelogram ABCD such that l(BC) = 7 cm, m∠ABC = 40° , l(AB) = 3 cm.
Given: Parallelogram ABCD in which diagonals AC and BD intersect at M.
Prove: M is the mid-point of LN.
ABCD is a parallelogram. What kind of quadrilateral is it if: AC = BD but AC is not perpendicular to BD?
In parallelogram ABCD, E is the mid-point of side AB and CE bisects angle BCD. Prove that :
(i) AE = AD,
(ii) DE bisects and ∠ADC and
(iii) Angle DEC is a right angle.
Iron rods a, b, c, d, e, and f are making a design in a bridge as shown in the figure. If a || b, c || d, e || f, find the marked angles between d and e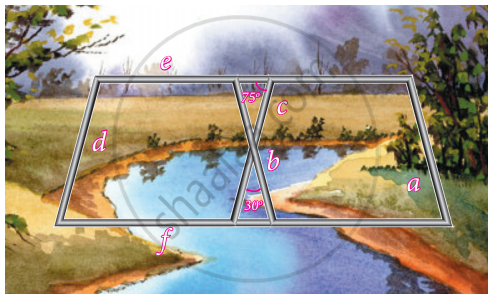
If opposite angles of a quadrilateral are equal, it must be a parallelogram.
The angle between the two altitudes of a parallelogram through the vertex of an obtuse angle of the parallelogram is 45°. Find the angles of the parallelogram.
