Advertisements
Advertisements
प्रश्न
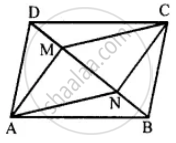
Given: Parallelogram ABCD in which diagonals AC and BD intersect at M.
Prove: M is the mid-point of LN.
उत्तर

Proof: Diagonals of //gm bisect each other.
MD = MB
Also ∠ADB = ∠DBN (Alternate ∠s)
& ∠DML = ∠BMN (Vert. opp. ∠s)
∆DML = ∆BMN
LM = MN
M is mid-point of LN.
Hence proved.
APPEARS IN
संबंधित प्रश्न
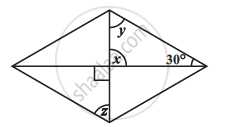
Consider the given parallelograms. Find the values of the unknowns x, y, z.
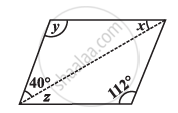
Consider the given parallelograms. Find the values of the unknowns x, y, z.
In the given figure, if points P, Q, R, S are on the sides of parallelogram such that AP = BQ = CR = DS then prove that `square`PQRS is a parallelogram.

Construct ☐ BARC such that l(BA) = l(BC) = 4.2 cm, l(AC) = 6.0 cm, l(AR) = l(CR) = 5.6 cm
ABCD is a parallelogram. What kind of quadrilateral is it if: AC = BD but AC is not perpendicular to BD?
In parallelogram ABCD, E is the mid-point of AD and F is the mid-point of BC. Prove that BFDE is a parallelogram.
The given figure shows parallelogram ABCD. Points M and N lie in diagonal BD such that DM = BN.
Prove that:
(i) ∆DMC = ∆BNA and so CM = AN
(ii) ∆AMD = ∆CNB and so AM CN
(iii) ANCM is a parallelogram.
Which of the following figures satisfy the following properties?
- All sides are congruent.
- All angles are right angles.
- Opposite sides are parallel.
In the given figure, ABCD and BDCE are parallelograms with common base DC. If BC ⊥ BD, then ∠BEC = ______.

Construct a parallelogram when one of its side is 4 cm and its two diagonals are 5.6 cm and 7 cm. Measure the other side.
