Advertisements
Advertisements
प्रश्न
In the given figure, ABCD and BDCE are parallelograms with common base DC. If BC ⊥ BD, then ∠BEC = ______.

विकल्प
60°
30°
150°
120°
उत्तर
In the given figure, ABCD and BDCE are parallelograms with common base DC. If BC ⊥ BD, then ∠BEC = 60°.
Explanation:

Given: ∠BAD = 30°
So, ∠BCD = 30° ...[Opposite angles of a parallelogram are equal]
Now, In triangle CBD:
∠DBC + ∠BCD + ∠CDB = 180° ...[Sum of all angles of a triangle is equal to 180°]
90° + 30° + ∠CDB = 180°
∠CDB = 180° – 90° – 30°
∠CDB = 180° – 120°
∠CDB = 60°
Therefore, ∠BEC = 60° ...[Opposite angles of a parallelogram are equal]
APPEARS IN
संबंधित प्रश्न
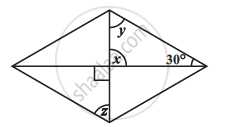
Consider the given parallelograms. Find the values of the unknowns x, y, z.
If the ratio of measures of two adjacent angles of a parallelogram is 1 : 2, find the measures of all angles of the parallelogram.
In the given figure, G is the point of concurrence of medians of ΔDEF. Take point H on ray DG such that D-G-H and DG = GH, then prove that `square`GEHF is a parallelogram.

Construct ☐ PQRS, such that l(PQ) = 3.5 cm, l(QR) = 5.6 cm, l(RS) = 3.5 cm, m∠Q = 110°, m∠R = 70°. If it is given that ☐ PQRS is a parallelogram, which of the given information is unnecessary?
Referring the adjacent figure of a parallelogram, write the answer of questions given below.
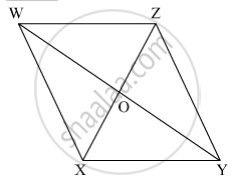
(1) If l(WZ) = 4.5 cm then l(XY) = ?
(2) If l(YZ) = 8.2 cm then l(XW) = ?
(3) If l(OX) = 2.5 cm then l(OZ) = ?
(4) If l(WO) = 3.3 cm then l(WY) = ?
(5) If m∠WZY = 120° then m∠WXY = ? and m∠XWZ = ?
The given figure shows parallelogram ABCD. Points M and N lie in diagonal BD such that DM = BN.
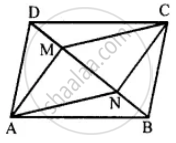
Prove that:
(i) ∆DMC = ∆BNA and so CM = AN
(ii) ∆AMD = ∆CNB and so AM CN
(iii) ANCM is a parallelogram.
Which of the following is a property of a parallelogram?
The angle between the two altitudes of a parallelogram through the same vertex of an obtuse angle of the parallelogram is 30°. The measure of the obtuse angle is ______.
All rectangles are parallelograms.
In parallelogram LOST, SN ⊥ OL and SM ⊥ LT. Find ∠STM, ∠SON and ∠NSM.

