Advertisements
Advertisements
Question
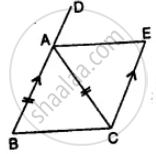
In the given figure, ABCD and BDCE are parallelograms with common base DC. If BC ⊥ BD, then ∠BEC = ______.

Options
60°
30°
150°
120°
Solution
In the given figure, ABCD and BDCE are parallelograms with common base DC. If BC ⊥ BD, then ∠BEC = 60°.
Explanation:

Given: ∠BAD = 30°
So, ∠BCD = 30° ...[Opposite angles of a parallelogram are equal]
Now, In triangle CBD:
∠DBC + ∠BCD + ∠CDB = 180° ...[Sum of all angles of a triangle is equal to 180°]
90° + 30° + ∠CDB = 180°
∠CDB = 180° – 90° – 30°
∠CDB = 180° – 120°
∠CDB = 60°
Therefore, ∠BEC = 60° ...[Opposite angles of a parallelogram are equal]
APPEARS IN
RELATED QUESTIONS
In the given figure, G is the point of concurrence of medians of ΔDEF. Take point H on ray DG such that D-G-H and DG = GH, then prove that `square`GEHF is a parallelogram.

In the given figure, if points P, Q, R, S are on the sides of parallelogram such that AP = BQ = CR = DS then prove that `square`PQRS is a parallelogram.

Ratio of two adjacent sides of a parallelogram is 3 : 4, and its perimeter is 112 cm. Find the length of its each side.
Prove that the diagonals of a parallelogram bisect each other.
In parallelogram ABCD, E is the mid-point of side AB and CE bisects angle BCD. Prove that :
(i) AE = AD,
(ii) DE bisects and ∠ADC and
(iii) Angle DEC is a right angle.
In the given figure, AB || EC, AB = AC and AE bisects ∠DAC. Prove that:
- ∠EAC = ∠ACB
- ABCE is a parallelogram.
Which of the following is a property of a parallelogram?
If two adjacent angles of a parallelogram are (5x – 5)° and (10x + 35)°, then the ratio of these angles is ______.
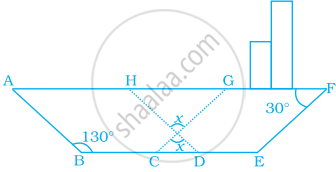
In the following figure of a ship, ABDH and CEFG are two parallelograms. Find the value of x.
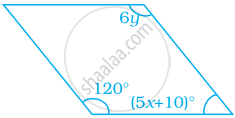
Find the values of x and y in the following parallelogram.