Advertisements
Advertisements
Question
In the given figure, if points P, Q, R, S are on the sides of parallelogram such that AP = BQ = CR = DS then prove that `square`PQRS is a parallelogram.

Solution
Given: `square` ABCD is a parallelogram.
AP = BQ = CR = DS
To prove: `square`PQRS is a parallelogram.
Proof:
AP = CR ...(Given) ...(i)
`square`ABCD is a parallelogram.
AB = CD ...(opposite sides of parallelogram)
∴ AP + PB = CR + RD ...[A-P-B, D-R-C] ...(ii)
∴ PB = RD ...[From (i) and (ii)] ...(iii)
∠ABC ≅ ∠ADC ...(Opposite angles of parallelogram)
That is, ∠PBQ ≅ ∠RDS ...(A-P-B, B-Q-C, C-R-D and A-S-D) ...(iv)
In ΔPBQ and ΔRDS,
Seg PB ≅ Seg RD ...[From (iii)]
∠PBQ ≅ ∠RDS ...[From (iv)]
Seg BQ ≅ Seg SD ...(Given)
∴ ΔPBQ ≅ ΔRDS ...[SAS test]
Seg PQ ≅ Seg RS ...(c.s.c.t) ...(v)
Thus, we can prove that, ΔPAS ≅ ΔRCQ,
∴ Seg PS ≅ Seg RQ ...(vi)
In `square`PQRS,
Seg PQ ≅ Seg RS ...[From (v)]
Seg PS ≅ Seg RQ ...[from (vi)]
If the opposite sides of a quadrilateral are congruent, then it is a parallelogram.
∴ `square`PQRS is a parallelogram.
APPEARS IN
RELATED QUESTIONS
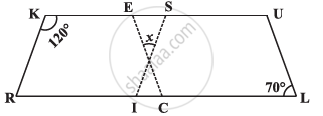
In the above figure both RISK and CLUE are parallelograms. Find the value of x.
ABCD is a parallelogram. What kind of quadrilateral is it if: AC = BD but AC is not perpendicular to BD?
In parallelogram ABCD, X and Y are midpoints of opposite sides AB and DC respectively. Prove that:
(i) AX = YC
(ii) AX is parallel to YC
(iii) AXCY is a parallelogram.
If a triangle and a parallelogram lie on the same base and between the same parallels, then prove that the area of the triangle is equal to half of the area of parallelogram
Which of the following figures satisfy the following properties?
- All sides are congruent.
- All angles are right angles.
- Opposite sides are parallel.
All rectangles are parallelograms.
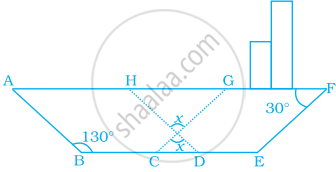
In the following figure of a ship, ABDH and CEFG are two parallelograms. Find the value of x.
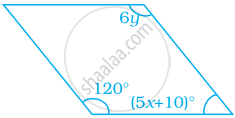
Find the values of x and y in the following parallelogram.
ABCD is a parallelogram. The bisector of angle A intersects CD at X and bisector of angle C intersects AB at Y. Is AXCY a parallelogram? Give reason.
Draw a rough figure of a quadrilateral that is not a parallelogram but has exactly two opposite angles of equal measure.
