Advertisements
Advertisements
प्रश्न
In the given figure, if points P, Q, R, S are on the sides of parallelogram such that AP = BQ = CR = DS then prove that `square`PQRS is a parallelogram.

उत्तर
Given: `square` ABCD is a parallelogram.
AP = BQ = CR = DS
To prove: `square`PQRS is a parallelogram.
Proof:
AP = CR ...(Given) ...(i)
`square`ABCD is a parallelogram.
AB = CD ...(opposite sides of parallelogram)
∴ AP + PB = CR + RD ...[A-P-B, D-R-C] ...(ii)
∴ PB = RD ...[From (i) and (ii)] ...(iii)
∠ABC ≅ ∠ADC ...(Opposite angles of parallelogram)
That is, ∠PBQ ≅ ∠RDS ...(A-P-B, B-Q-C, C-R-D and A-S-D) ...(iv)
In ΔPBQ and ΔRDS,
Seg PB ≅ Seg RD ...[From (iii)]
∠PBQ ≅ ∠RDS ...[From (iv)]
Seg BQ ≅ Seg SD ...(Given)
∴ ΔPBQ ≅ ΔRDS ...[SAS test]
Seg PQ ≅ Seg RS ...(c.s.c.t) ...(v)
Thus, we can prove that, ΔPAS ≅ ΔRCQ,
∴ Seg PS ≅ Seg RQ ...(vi)
In `square`PQRS,
Seg PQ ≅ Seg RS ...[From (v)]
Seg PS ≅ Seg RQ ...[from (vi)]
If the opposite sides of a quadrilateral are congruent, then it is a parallelogram.
∴ `square`PQRS is a parallelogram.
APPEARS IN
संबंधित प्रश्न
Given a parallelogram ABCD. Complete each statement along with the definition or property used.
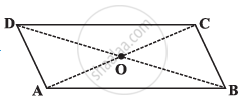
- AD = ______
- ∠DCB = ______
- OC = ______
- m∠DAB + m∠CDA = ______
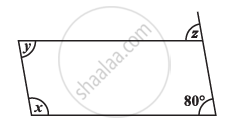
Consider the given parallelograms. Find the values of the unknowns x, y, z.
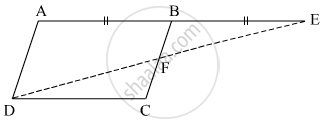
In the given figure, `square`ABCD is a parallelogram. Point E is on the ray AB such that BE = AB then prove that line ED bisects seg BC at point F.
PQRS is a parallelogram whose diagonals intersect at M.
If ∠PMS = 54°, ∠QSR = 25° and ∠SQR = 30° ; find :
(i) ∠RPS
(ii) ∠PRS
(iii) ∠PSR.
ABCD is a parallelogram. What kind of quadrilateral is it if : AC = BD and AC is perpendicular to BD?
In parallelogram ABCD, E is the mid-point of AD and F is the mid-point of BC. Prove that BFDE is a parallelogram.
The given figure shows parallelogram ABCD. Points M and N lie in diagonal BD such that DM = BN.
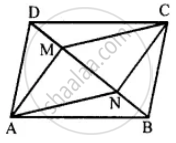
Prove that:
(i) ∆DMC = ∆BNA and so CM = AN
(ii) ∆AMD = ∆CNB and so AM CN
(iii) ANCM is a parallelogram.
In parallelogram MODE, the bisector of ∠M and ∠O meet at Q, find the measure of ∠MQO.
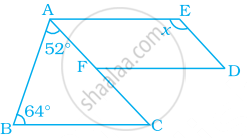
In the following figure, FD || BC || AE and AC || ED. Find the value of x.
Construct a parallelogram ABCD in which AB = 4 cm, BC = 5 cm and ∠B = 60°.
