Advertisements
Advertisements
प्रश्न
The given figure shows parallelogram ABCD. Points M and N lie in diagonal BD such that DM = BN.
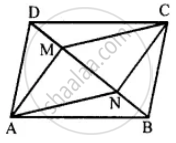
Prove that:
(i) ∆DMC = ∆BNA and so CM = AN
(ii) ∆AMD = ∆CNB and so AM CN
(iii) ANCM is a parallelogram.
उत्तर
Given: In parallelogram ABCD, points M and N lie on the diagonal BD such that DM = BN
AN, NC, CM and MA are joined
To prove :
(i) ∆DMC = ∆BNA and so CM = AN
(ii) ∆AMD = ∆CNB and so AM = CN
(iii) ANCM is a parallelogram
Proof :
(i) In ∆DMC and ∆BNA.
CD = AB (opposite sides of ||gm ABCD)
DM = BN (given)
∠CDM = ∠ABN (alternate angles)
∆DMC = ∆BNA (SAS axiom)
CM =AN (c.p.c.t.)
Similarly, in ∆AMD and ∆CNB
AD = BC (opposite sides of ||gm)
DM = BN (given)
∠ADM = ∠CBN – (alternate angles)
∆AMD = ∆CNB (SAS axiom)
AM = CN (c.p.c.t.)
(iii) CM = AN and AM = CN (proved)
ANCM is a parallelogram (opposite sides are equal)
Hence proved.
APPEARS IN
संबंधित प्रश्न
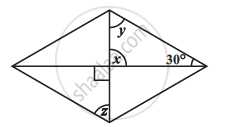
Consider the given parallelogram. Find the values of the unknowns x, y, z.

Consider the given parallelograms. Find the values of the unknowns x, y, z.
Can a quadrilateral ABCD be a parallelogram if AB = DC = 8 cm, AD = 4 cm and BC = 4.4 cm?
Two adjacent angles of a parallelogram have equal measure. Find the measure of each of the angles of the parallelogram.
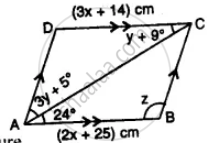
Use the information given in the alongside diagram to find the value of x, y, and z.
In parallelogram LOST, SN ⊥ OL and SM ⊥ LT. Find ∠STM, ∠SON and ∠NSM.

In parallelogram MODE, the bisector of ∠M and ∠O meet at Q, find the measure of ∠MQO.
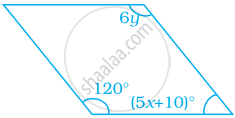
Find the values of x and y in the following parallelogram.
Construct a parallelogram ABCD in which AB = 4 cm, BC = 5 cm and ∠B = 60°.
Construct a parallelogram HOME with HO = 6 cm, HE = 4 cm and OE = 3 cm.
