Advertisements
Advertisements
प्रश्न
The given figure shows a rhombus ABCD in which angle BCD = 80°. Find angles x and y.
Advertisements
उत्तर
In rhombus ABCD, diagonals AC and BD bisect each other at 90°
∠BCD = 80°
Diagonals bisect the opposite angles also ∠BCD =
∠BAD (Opposite angles of rhombus)
∠BAD = 80° and ∠ABC = ∠ADC = 180° – 80° = 100°
Diagonals bisect opposite angles
∠OCB or ∠PCB =`80^circ/2` = 40°
In ∆PCM,
Ext. CPD = ∠OCB + ∠PMC
110° = 40° + x
⇒ x = 110° – 40° = 70°
and ∠ADO = `1/2` ∠ADC = `1/2 xx 100^circ = 50^circ`
Hence x = 70° and y = 50°
APPEARS IN
संबंधित प्रश्न
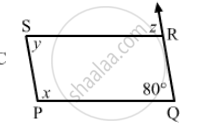
The following figure is parallelogram. Find the degree values of the unknown x, y, z.
Can the following figure be parallelogram. Justify your answer.
The measure of one angle of a parallelogram is 70°. What are the measures of the remaining angles?
Which of the following statement is true for a rhombus?
It has two pairs of equal sides.
Fill in the blank, in the following, so as to make the statement true:
The diagonals of a rhombus ...... each other at ...... angles.
Draw a rhombus, having each side of length 3.5 cm and one of the angles as 40°.
Diagonals of a rhombus are 20 cm and 21 cm respectively, then find the side of rhombus and its perimeter.
State with reason whether the following statement is ‘true’ or ‘false’.
Every rhombus is a rectangle.
If a diagonal of a quadrilateral bisects both the angles, then it is a ______.
Diagonals of a quadrilateral are perpendicular to each other. Is such a quadrilateral always a rhombus? Give a figure to justify your answer.
