Advertisements
Advertisements
प्रश्न
ABCD is a rhombus. If ∠BCA = 35°. find ∠ADC.
उत्तर
Given : Rhombus ABCD in which ∠BCA = 35°
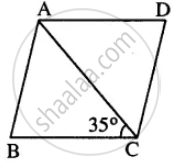
To find : ∠ADC
Proof : AD || BC
∠DAC = ∠BCA (Alternate ∠s)
But ∠BCA = 35° (Given)
∠DAC = 35°
But ∠DAC = ∠ACD ( AD = CD) & ∠DAC +∠ACD + ∠ADC = 180°
35°+ 35° + ∠ADC = 180°
∠ADC = 180° – 70° = 110°
Hence ∠ADC = 110°
APPEARS IN
संबंधित प्रश्न
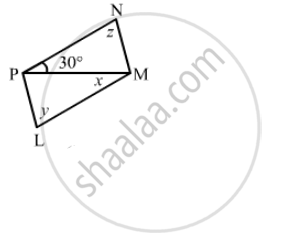
The following figure is parallelogram. Find the degree values of the unknown x, y, z.
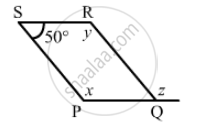
The following figure is parallelogram. Find the degree values of the unknown x, y, z.
In the following Figure ABCD is a arallelogram, CE bisects ∠C and AF bisects ∠A. In each of the following, if the statement is true, give a reason for the same:
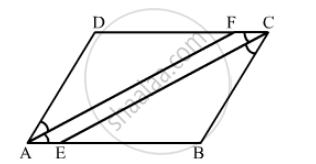
(i) ∠A = ∠C
(ii) \[\angle FAB = \frac{1}{2}\angle A\]
(iii) \[\angle DCE = \frac{1}{2}\angle C\]
(iv) \[\angle CEB = \angle FAB\]
(v) CE || AF
Which of the following statement is true for a rhombus?
It has two pairs of parallel sides.
Which of the following statement is true for a rhombus?
Its diagonals bisect each other at right angles.
ABCD is a rhombus. If ∠ACB = 40°, find ∠ADB.
ABCD is a rhombus and its diagonals intersect at O.
(i) Is ∆BOC ≅ ∆DOC? State the congruence condition used?
(ii) Also state, if ∠BCO = ∠DCO.
A quadrilateral whose all sides are equal, opposite angles are equal and the diagonals bisect each other at right angles is a ______.
If a diagonal of a quadrilateral bisects both the angles, then it is a ______.
In a rhombus diagonals intersect at ______ angles.
