Advertisements
Advertisements
प्रश्न
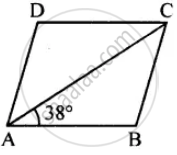
ABCD is a rhombus. If ∠BAC = 38°, find :
(i) ∠ACB
(ii) ∠DAC
(iii) ∠ADC.
उत्तर
ABCD is Rhombus (Given)
AB = BC
∠BAC = ∠ACB (∠s opp. to equal sides)
But ∠BAC = 38° (Given)
∠ACB = 38°
In ∆ABC,
∠ABC + ∠BAC + ∠ACB = 180°
∠ABC + 38°+ 38° = 180°
∠ABC = 180° – 76° = 104°
But ∠ABC = ∠ADC (opp. ∠s of rhombus)
∠ADC = 104°
∠DAC = ∠DCA ( AD = CD)
∠DAC = `1/2` [180° - 104°]
∠DAC = `1/2 xx` 76° = 38°
Hence (i) ∠ACB = 38° (ii) ∠DAC = 38° (iii) ∠ADC = 104° Ans.
APPEARS IN
संबंधित प्रश्न
Can the following figure be parallelogram. Justify your answer.
If an angle of a parallelogram is two-third of its adjacent angle, find the angles of the parallelogram.
The sum of two opposite angles of a parallelogram is 130°. Find all the angles of the parallelogram.
All the angles of a quadrilateral are equal to each other. Find the measure of each. Is the quadrilateral a parallelogram? What special type of parallelogram is it?
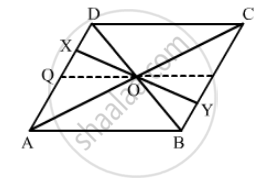
Diagonals of parallelogram ABCD intersect at O as shown in the following fegure. XY contains O, and X, Y are points on opposite sides of the parallelogram. Give reasons for each of the following:
(i) OB = OD
(ii) ∠OBY = ∠ODX
(iii) ∠BOY = ∠DOX
(iv) ∆BOY ≅ ∆DOX
Now, state if XY is bisected at O.
Which of the following statement is true for a rhombus?
It has all its sides of equal lengths.
Fill in the blank, in the following, so as to make the statement true:
A rhombus is a parallelogram in which ......
Identify all the quadrilateral that have Four sides of equal length
Diagonals of a parallelogram intersect each other at point O. If AO = 5, BO = 12 and AB = 13 then show that `square`ABCD is a rhombus.
Diagonals of a rhombus are 20 cm and 21 cm respectively, then find the side of rhombus and its perimeter.
