Advertisements
Advertisements
प्रश्न
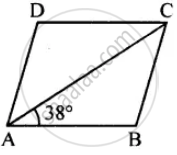
ABCD is a rhombus. If ∠BAC = 38°, find :
(i) ∠ACB
(ii) ∠DAC
(iii) ∠ADC.
उत्तर
ABCD is Rhombus (Given)
AB = BC
∠BAC = ∠ACB (∠s opp. to equal sides)
But ∠BAC = 38° (Given)
∠ACB = 38°
In ∆ABC,
∠ABC + ∠BAC + ∠ACB = 180°
∠ABC + 38°+ 38° = 180°
∠ABC = 180° – 76° = 104°
But ∠ABC = ∠ADC (opp. ∠s of rhombus)
∠ADC = 104°
∠DAC = ∠DCA ( AD = CD)
∠DAC = `1/2` [180° - 104°]
∠DAC = `1/2 xx` 76° = 38°
Hence (i) ∠ACB = 38° (ii) ∠DAC = 38° (iii) ∠ADC = 104° Ans.
APPEARS IN
संबंधित प्रश्न
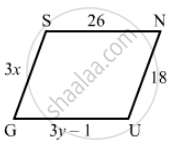
In the following figure GUNS and RUNS are parallelogram. Find x and y.
In the following Figure ABCD is a arallelogram, CE bisects ∠C and AF bisects ∠A. In each of the following, if the statement is true, give a reason for the same:
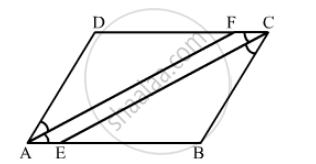
(i) ∠A = ∠C
(ii) \[\angle FAB = \frac{1}{2}\angle A\]
(iii) \[\angle DCE = \frac{1}{2}\angle C\]
(iv) \[\angle CEB = \angle FAB\]
(v) CE || AF
Points E and F lie on diagonal AC of a parallelogram ABCD such that AE = CF. What type of quadrilateral is BFDE?
Which of the following statement is true for a rhombus?
Two of its angles are at right angles
Which of the following statement is true for a rhombus?
It is a square.
Fill in the blank, in each of the following, so as to make the statement true:
If the diagonals of a parallelogram bisect each other at right angles, then it is a ......
The diagonals of a parallelogram are not perpendicular. Is it a rhombus? Why or why not?
Draw a rhombus, having each side of length 3.5 cm and one of the angles as 40°.
ABCD is a rhombus and its diagonals intersect at O.
(i) Is ∆BOC ≅ ∆DOC? State the congruence condition used?
(ii) Also state, if ∠BCO = ∠DCO.
A rhombus is a parallelogram in which ______ sides are equal.
