Advertisements
Advertisements
प्रश्न
ABCD is a rhombus and its diagonals intersect at O.
(i) Is ∆BOC ≅ ∆DOC? State the congruence condition used?
(ii) Also state, if ∠BCO = ∠DCO.
उत्तर
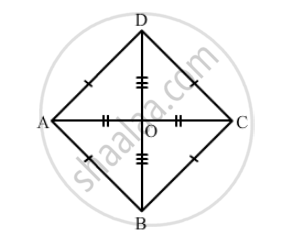
(i) Yes
\[\text{ In } ∆ BCO \text{ and } ∆ DCO: \]
\[OC = OC (\text{ common })\]
\[BC = DC (\text{ all sides of a rhombus are equal })\]
\[BO = OD (\text{ diagonals of a rhomus bisect each other })\]
\[\text{ By SSS congruence }: \]
\[ ∆ BCO \cong ∆ DCO\]
Yes
By c.p.c.t:
\[\angle BCO = \angle DCO\]
APPEARS IN
संबंधित प्रश्न
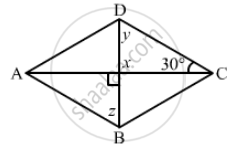
The following figure is parallelogram. Find the degree values of the unknowns x, y, z.
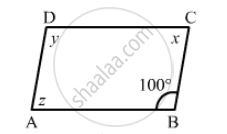
The following figure is parallelogram. Find the degree values of the unknown x, y, z.
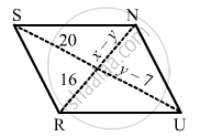
In the following figure GUNS and RUNS are parallelogram. Find x and y.
The sum of two opposite angles of a parallelogram is 130°. Find all the angles of the parallelogram.
Fill in the blank, in the following, so as to make the statement true:
The diagonals of a rhombus ...... each other at ...... angles.
If the diagonals of a rhombus are 12 cm and 16cm, find the length of each side.
ABCD is a rhombus whose diagonals intersect at O. If AB = 10 cm, diagonal BD = 16 cm, find the length of diagonal AC.
State with reason whether the following statement is ‘true’ or ‘false’.
Every rhombus is a rectangle.
If all pairs of adjacent sides of a quadrilateral are congruent then it is called ______.
The lengths of the diagonals of a Rhombus are 12 cm and 16 cm. Find the side of the rhombus
