Advertisements
Advertisements
Question
ABCD is a rhombus and its diagonals intersect at O.
(i) Is ∆BOC ≅ ∆DOC? State the congruence condition used?
(ii) Also state, if ∠BCO = ∠DCO.
Solution
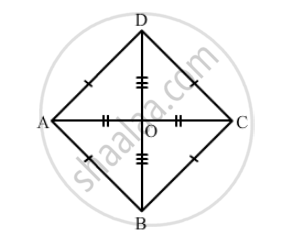
(i) Yes
\[\text{ In } ∆ BCO \text{ and } ∆ DCO: \]
\[OC = OC (\text{ common })\]
\[BC = DC (\text{ all sides of a rhombus are equal })\]
\[BO = OD (\text{ diagonals of a rhomus bisect each other })\]
\[\text{ By SSS congruence }: \]
\[ ∆ BCO \cong ∆ DCO\]
Yes
By c.p.c.t:
\[\angle BCO = \angle DCO\]
APPEARS IN
RELATED QUESTIONS
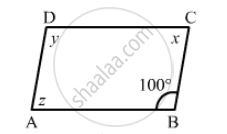
The following figure is parallelogram. Find the degree values of the unknowns x, y, z.
The measure of one angle of a parallelogram is 70°. What are the measures of the remaining angles?
The sum of two opposite angles of a parallelogram is 130°. Find all the angles of the parallelogram.
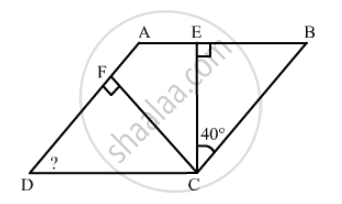
Find the angles marked with a question mark shown in Fig. 17.27
Points E and F lie on diagonal AC of a parallelogram ABCD such that AE = CF. What type of quadrilateral is BFDE?
One side of a rhombus is of length 4 cm and the length of an altitude is 3.2 cm. Draw the rhombus.
State with reason whether the following statement is ‘true’ or ‘false’.
Every parallelogram is a rhombus.
Diagonals PR and QS of a rhombus PQRS are 20 cm and 48 cm respectively. Find the length of side PQ.
Lengths of diagonals of a rhombus ABCD are 16 cm and 12 cm. Find the side and perimeter of the rhombus.
Construct a rhombus whose side is 5 cm and one angle is of 60°.
