Advertisements
Advertisements
Question
Points E and F lie on diagonal AC of a parallelogram ABCD such that AE = CF. What type of quadrilateral is BFDE?
Solution

\[AO = OC . . . . . . (i) (\text{ diagonals of a parallelogram bisect each other })\]
\[AE = CF . . . . . . . (ii) (\text{ given })\]
\[\text{ Subtracting (ii) from } (i): \]
\[AO - AE = OC - CF\]
\[EO = OF . . . . . . . . . (iii)\]
\[\text{ In } ∆ DOE \text{ and } ∆ BOF: \]
\[EO = OF (\text{ proved above })\]
\[DO = OB (\text{ diagonals of a parallelogram bisect each other })\]
\[\angle DOE = \angle BOF (\text{ vertically opposite angles })\]
\[\text{ By SAS congruence }: \]
\[ ∆ DOE \cong ∆ BOF\]
\[ \therefore DE = BF (c . p . c . t)\]
\[\text{ In } ∆ BOE \text{ and } ∆ DOF: \]
\[EO = OF (\text{ proved above })\]
\[DO = OB (\text{ diagonals of a parallelogram bisect each other })\]
\[\angle DOF = \angle BOE (\text{ vertically opposite angles })\]
\[\text{ By SAS congruence }: \]
\[ ∆ DOE \cong ∆ BOF\]
\[ \therefore DF = BE (c . p . c . t)\]
\[\text{ Hence, the pair of opposite sides are equal . Thus, DEBF is a parallelogram }. \]
APPEARS IN
RELATED QUESTIONS
The following figure is parallelogram. Find the degree values of the unknown x, y, z.
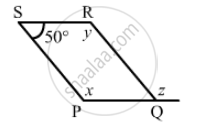
The following figure is parallelogram. Find the degree values of the unknown x, y, z.
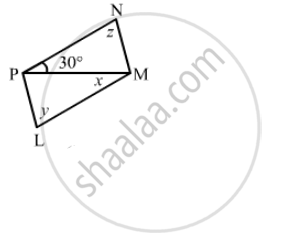
Two adjacent angles of a parallelogram are as 1 : 2. Find the measures of all the angles of the parallelogram.
Which of the following statement is true for a rhombus?
Its diagonals are equal and perpendicular.
ABCD is a rhombus. If ∠ACB = 40°, find ∠ADB.
Construct a rhombus whose diagonals are of length 10 cm and 6 cm.
ABCD is a rhombus. If ∠BAC = 38°, find :
(i) ∠ACB
(ii) ∠DAC
(iii) ∠ADC.
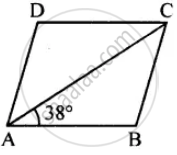
The lengths of the diagonals of a Rhombus are 12 cm and 16 cm. Find the side of the rhombus
If the diagonal of a rhombus are equal, then the rhombus is a
Construct a rhombus whose side is 5 cm and one angle is of 60°.
