Advertisements
Advertisements
Question
ABCD is a rhombus. If ∠ACB = 40°, find ∠ADB.
Solution
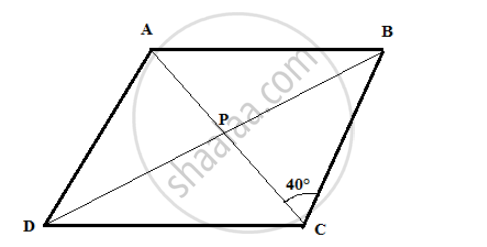
\[\text{ In a rhombus, the diagonals are perpendicular } . \]
\[ \therefore \angle BPC = 90°\]
\[\text{ From ∆ BPC, the sum of angles is }180° . \]
\[ \therefore \angle CBP + \angle BPC + \angle PBC = 180°\]
\[\angle CBP = 180° - \angle BPC - \angle PBC\]
\[\angle CBP = 180° - 40° - 90° = 50° \]
\[\angle ADB = \angle CBP = 50°(\text{ alternate angle })\]
APPEARS IN
RELATED QUESTIONS
Name the quadrilaterals whose diagonals are perpendicular bisectors of each other
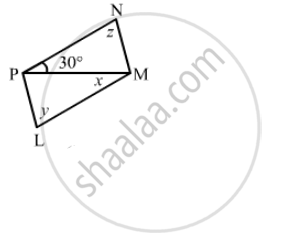
The following figure is parallelogram. Find the degree values of the unknown x, y, z.
Can the following figure be parallelogram. Justify your answer.
ABCD is a parallelogram in which ∠A = 70°. Compute ∠B, ∠C and ∠D.
The perimeter of a parallelogram is 150 cm. One of its sides is greater than the other by 25 cm. Find the length of the sides of the parallelogram.
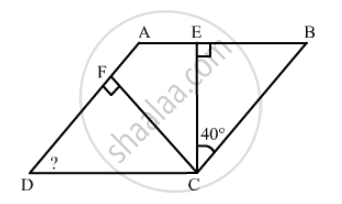
Find the angles marked with a question mark shown in Fig. 17.27
Which of the following statement is true for a rhombus?
It has two pairs of parallel sides.
Which of the following statement is true for a rhombus?
Its diagonals bisect each other at right angles.
Which of the following statement is true for a rectangle?
Its diagonals are equal and bisect each other.
Draw a rhombus KLMN such that its side is 4 cm and m∠K = 75°.
