Advertisements
Advertisements
प्रश्न
ABCD is a rhombus. If ∠ACB = 40°, find ∠ADB.
Advertisements
उत्तर
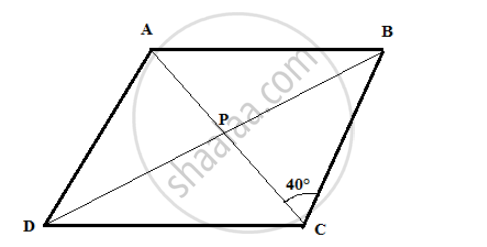
\[\text{ In a rhombus, the diagonals are perpendicular } . \]
\[ \therefore \angle BPC = 90°\]
\[\text{ From ∆ BPC, the sum of angles is }180° . \]
\[ \therefore \angle CBP + \angle BPC + \angle PBC = 180°\]
\[\angle CBP = 180° - \angle BPC - \angle PBC\]
\[\angle CBP = 180° - 40° - 90° = 50° \]
\[\angle ADB = \angle CBP = 50°(\text{ alternate angle })\]
APPEARS IN
संबंधित प्रश्न
In the following figure GUNS and RUNS are parallelogram. Find x and y.
Two adjacent angles of a parallelogram are as 1 : 2. Find the measures of all the angles of the parallelogram.
In the following Figure ABCD is a arallelogram, CE bisects ∠C and AF bisects ∠A. In each of the following, if the statement is true, give a reason for the same:
(i) ∠A = ∠C
(ii) \[\angle FAB = \frac{1}{2}\angle A\]
(iii) \[\angle DCE = \frac{1}{2}\angle C\]
(iv) \[\angle CEB = \angle FAB\]
(v) CE || AF
In a parallelogram ABCD, AB = 10 cm, AD = 6 cm. The bisector of ∠A meets DC in E, AEand BC produced meet at F. Find te length CF.
Fill in the blank, inthe following, so as to make the statement true:
A square is a rhombus in which .....
Fill in the blank, in the following, so as to make the statement true:
The diagonals of a rhombus ...... each other at ...... angles.
If the diagonals of a rhombus are 12 cm and 16cm, find the length of each side.
One side of a rhombus is of length 4 cm and the length of an altitude is 3.2 cm. Draw the rhombus.
In a rhombus diagonals intersect at ______ angles.
A rhombus is a parallelogram in which ______ sides are equal.
