Advertisements
Advertisements
प्रश्न
All the angles of a quadrilateral are equal to each other. Find the measure of each. Is the quadrilateral a parallelogram? What special type of parallelogram is it?
उत्तर
\[\text{ Let the angle be x }. \]
\[\text{ All the angles are equal .} \]
\[ \therefore x + x + x + x = 360°\]
\[4x = 360°\]
\[x = 90°\]
\[\text{ So, each angle is 90°and quadrilateral is a parallelogram . It is a rectangle } .\]
APPEARS IN
संबंधित प्रश्न
Can the following figure be parallelogram. Justify your answer.
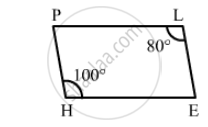
In the following figure RISK and CLUE are parallelograms. Find the measure of x.
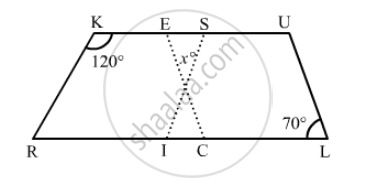
Two adjacent angles of a parallelogram are as 1 : 2. Find the measures of all the angles of the parallelogram.
ABCD is a parallelogram in which ∠A = 70°. Compute ∠B, ∠C and ∠D.
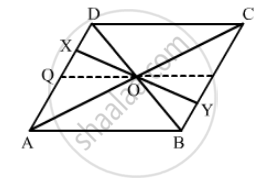
Diagonals of parallelogram ABCD intersect at O as shown in the following fegure. XY contains O, and X, Y are points on opposite sides of the parallelogram. Give reasons for each of the following:
(i) OB = OD
(ii) ∠OBY = ∠ODX
(iii) ∠BOY = ∠DOX
(iv) ∆BOY ≅ ∆DOX
Now, state if XY is bisected at O.
Which of the following statement is true for a rhombus?
Its diagonals bisect each other at right angles.
Which of the following statement is true for a rhombus?
It can be a square.
One side of a rhombus is of length 4 cm and the length of an altitude is 3.2 cm. Draw the rhombus.
The lengths of the diagonals of a Rhombus are 12 cm and 16 cm. Find the side of the rhombus
ABCD is a rhombus such that the perpendicular bisector of AB passes through D. Find the angles of the rhombus.
Hint: Join BD. Then ∆ABD is equilateral.
