Advertisements
Advertisements
प्रश्न
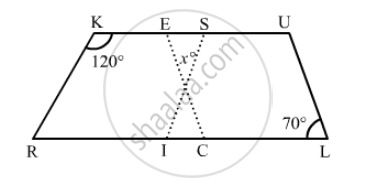
In the following figure RISK and CLUE are parallelograms. Find the measure of x.
उत्तर
\[\text{ In the parallelogram RISK }: \]
\[\angle ISK + \angle RKS = 180° (\text{ sum of adjacent angles of a parallelogram is } 180°\]
\[\angle ISK = 180° - 120° = 60°\]
\[\text{ Similarly, in parallelogram CLUE }: \]
\[\angle CEU = \angle CLU = 70°(\text{ opposite angles of a parallelogram are equal })\]
\[\text{ In the triangle }: \]
\[x + \angle ISK + \angle CEU = 180°\]
\[x = 180° - \left( 70°+ 60° \right)\]
\[x = 180°- \left( 70°+ 60°\right) = 50°\]
APPEARS IN
संबंधित प्रश्न
Name the quadrilaterals whose diagonals are perpendicular bisectors of each other
Can the following figure be parallelogram. Justify your answer.
The sum of two opposite angles of a parallelogram is 130°. Find all the angles of the parallelogram.
In the following Figure ABCD is a arallelogram, CE bisects ∠C and AF bisects ∠A. In each of the following, if the statement is true, give a reason for the same:
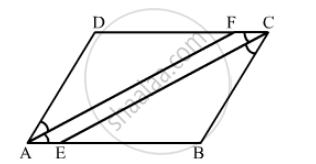
(i) ∠A = ∠C
(ii) \[\angle FAB = \frac{1}{2}\angle A\]
(iii) \[\angle DCE = \frac{1}{2}\angle C\]
(iv) \[\angle CEB = \angle FAB\]
(v) CE || AF
Which of the following statement is true for a rhombus?
It is a parallelogram.
ABCD is a rhombus and its diagonals intersect at O.
(i) Is ∆BOC ≅ ∆DOC? State the congruence condition used?
(ii) Also state, if ∠BCO = ∠DCO.
State with reason whether the following statement is ‘true’ or ‘false’.
Every rhombus is a rectangle.
If the adjacent sides of a parallelogram are equal then parallelogram is a ______.
Diagonals of a quadrilateral are perpendicular to each other. Is such a quadrilateral always a rhombus? Give a figure to justify your answer.
ABCD is a rhombus such that the perpendicular bisector of AB passes through D. Find the angles of the rhombus.
Hint: Join BD. Then ∆ABD is equilateral.
