Advertisements
Advertisements
प्रश्न
In the following Figure ABCD is a arallelogram, CE bisects ∠C and AF bisects ∠A. In each of the following, if the statement is true, give a reason for the same:
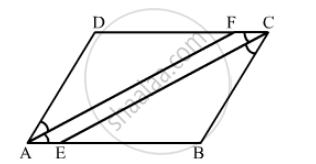
(i) ∠A = ∠C
(ii) \[\angle FAB = \frac{1}{2}\angle A\]
(iii) \[\angle DCE = \frac{1}{2}\angle C\]
(iv) \[\angle CEB = \angle FAB\]
(v) CE || AF
उत्तर
(i) True, since opposite angles of a parallelogram are equal.
(ii) True, as AF is the bisector of\[\angle\] A.
(iii) True, as CE is the bisector of \[\angle\]C.
(iv) True
\[\angle\]CEB =\[\angle\] DCE........(i) (alternate angles)
\[\angle\]DCE= \[\angle\] FAB.........(ii) (opposite angles of a parallelogram are equal)
From equations (i) and (ii):
\[\angle\] CEB =\[\angle\]FAB
(v) True, as corresponding angles are equal (\[\angle\] CEB =\[\angle\] FAB).
APPEARS IN
संबंधित प्रश्न
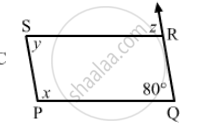
The following figure is parallelogram. Find the degree values of the unknown x, y, z.
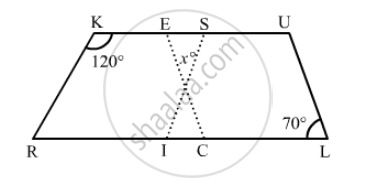
In the following figure RISK and CLUE are parallelograms. Find the measure of x.
All the angles of a quadrilateral are equal to each other. Find the measure of each. Is the quadrilateral a parallelogram? What special type of parallelogram is it?
Which of the following statement is true for a rhombus?
Its diagonals are equal and perpendicular.
Fill in the blank, in the following, so as to make the statement true:
A rhombus is a parallelogram in which ......
Fill in the blank, in the following, so as to make the statement true:
The diagonals of a rhombus ...... each other at ...... angles.
If the diagonals of a rhombus are 12 cm and 16cm, find the length of each side.
One side of a rhombus is of length 4 cm and the length of an altitude is 3.2 cm. Draw the rhombus.
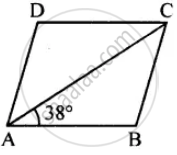
ABCD is a rhombus. If ∠BAC = 38°, find :
(i) ∠ACB
(ii) ∠DAC
(iii) ∠ADC.
The lengths of the diagonals of a Rhombus are 12 cm and 16 cm. Find the side of the rhombus
