Advertisements
Advertisements
प्रश्न
In the following Figure ABCD is a arallelogram, CE bisects ∠C and AF bisects ∠A. In each of the following, if the statement is true, give a reason for the same:
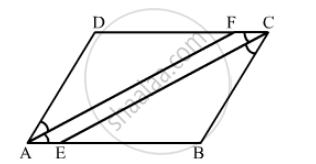
(i) ∠A = ∠C
(ii) \[\angle FAB = \frac{1}{2}\angle A\]
(iii) \[\angle DCE = \frac{1}{2}\angle C\]
(iv) \[\angle CEB = \angle FAB\]
(v) CE || AF
उत्तर
(i) True, since opposite angles of a parallelogram are equal.
(ii) True, as AF is the bisector of\[\angle\] A.
(iii) True, as CE is the bisector of \[\angle\]C.
(iv) True
\[\angle\]CEB =\[\angle\] DCE........(i) (alternate angles)
\[\angle\]DCE= \[\angle\] FAB.........(ii) (opposite angles of a parallelogram are equal)
From equations (i) and (ii):
\[\angle\] CEB =\[\angle\]FAB
(v) True, as corresponding angles are equal (\[\angle\] CEB =\[\angle\] FAB).
APPEARS IN
संबंधित प्रश्न
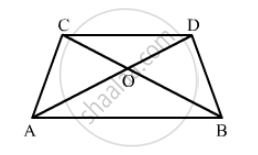
Given below is a parallelogram ABCD. Complete each statement along with the definition or property used.
(i) AD =
(ii) ∠DCB =
(iii) OC =
(iv) ∠DAB + ∠CDA =
Points E and F lie on diagonal AC of a parallelogram ABCD such that AE = CF. What type of quadrilateral is BFDE?
Which of the following statement is true for a rhombus?
It has two pairs of parallel sides.
Fill in the blank, inthe following, so as to make the statement true:
A square is a rhombus in which .....
Fill in the blank, in the following, so as to make the statement true:
The diagonals of a rhombus ...... each other at ...... angles.
Draw a rhombus, having each side of length 3.5 cm and one of the angles as 40°.
The diagonals of a quadrilateral are of lengths 6 cm and 8 cm. If the diagonals bisect each other at right angles, what is the length of each side of the quadrilateral?
Identify all the quadrilateral that have Four sides of equal length
ABCD is a rhombus such that the perpendicular bisector of AB passes through D. Find the angles of the rhombus.
Hint: Join BD. Then ∆ABD is equilateral.
Construct a rhombus CLUE in which CL = 7.5 cm and LE = 6 cm.
