Advertisements
Advertisements
प्रश्न
Diagonals of a parallelogram ABCD intersect at O. AL and CM are drawn perpendiculars to BD such that L and M lie on BD. Is AL = CM? Why or why not?
उत्तर

\[\text{ In } \Delta AOL \text{ and } \Delta CMO: \]
\[\angle AOL = \angle COM( \text{ vertically opposite angle }) . . . . (i)\]
\[\angle ALO = \angle CMO = 90° (\text{ each right angle }) . . . . . (ii)\]
\[\text{ Using angle sum property }: \]
\[\angle AOL + \angle ALO + \angle LAO = 180° . . . . . . . . . . (iii)\]
\[\angle COM + \angle CMO + \angle OCM = 180°. . . . . . (iv)\]
\[\text{ From equations } (iii) \text{ and } (iv): \]
\[\angle AOL + \angle ALO + \angle LAO = \angle COM + \angle CMO + \angle OCM\]
\[\angle LAO = \angle OCM (\text{ from equations (i) and } (ii) )\]
\[In \Delta AOL \text{ and }\Delta CMO: \]
\[\angle ALO = \angle CMO (\text{ each right angle })\]
\[AO = OC (\text{ diagonals of a parallelogram bisect each other })\]
\[\angle LAO = \angle OCM (\text{ proved above })\]
\[\text{ So }, \Delta AOL \text{ is congruent to } \Delta CMO (SAS) . \]
\[ \Rightarrow AL = CM [cpct]\]
APPEARS IN
संबंधित प्रश्न
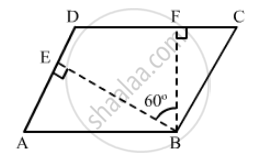
The angle between the altitudes of a parallelogram, through the same vertex of an obtuse angle of the parallelogram is 60°. Find the angles of the parallelogram.
Fill in the blank in the following, so as to make the statement true:
A rectangle is a parallelogram in which .....
In a rectangle ABCD, prove that ∆ACB ≅ ∆CAD.
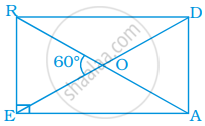
Diagonals of a rectangle PQRS are intersecting in point M. If ∠QMR = 50° find the measure of ∠MPS.
The following figure is a rectangle in which x: y = 3: 7; find the values of x and y.
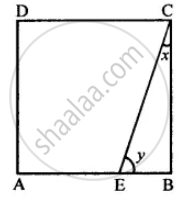
Show that the bisectors of angles of a parallelogram form a rectangle
All squares are rectangles.
PQRS is a rectangle. The perpendicular ST from S on PR divides ∠S in the ratio 2:3. Find ∠TPQ.
In rectangle READ, find ∠EAR, ∠RAD and ∠ROD
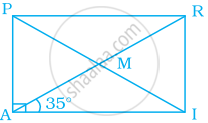
In rectangle PAIR, find ∠ARI, ∠RMI and ∠PMA.