Advertisements
Advertisements
प्रश्न
PQRS is a rectangle. The perpendicular ST from S on PR divides ∠S in the ratio 2:3. Find ∠TPQ.
उत्तर
Given, ST ⊥ PR and ST divides ∠S in the ratio 2:3
So, sum of ratio = 2 + 3 = 5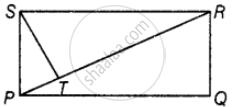
Now, `∠TSP = 2/5 xx 90^circ = 36^circ, ∠TSR = 3/5 xx 90^circ = 54^circ`
Also, by the angle sum property of a triangle,
∠TPS = 180° – (∠STP + ∠TSP)
= 180° – (90° + 36°)
= 54°
We know that, ∠SPQ = 90°
⇒ ∠TPS + ∠TPQ = 90°
⇒ 54° + ∠TPQ = 90°
⇒ ∠TPQ = 90° – 54° = 36°
APPEARS IN
संबंधित प्रश्न
Two adjacent angles of a parallelogram are (3x − 4)° and (3x + 10)°. Find the angles of the parallelogram.
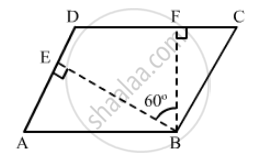
The angle between the altitudes of a parallelogram, through the same vertex of an obtuse angle of the parallelogram is 60°. Find the angles of the parallelogram.
Which of the following statement is true for a rectangle?
Its diagonals bisect each other.
Which of the following statement true for a square?
Its diagonals bisect each other at right angle.
Diagonals of a rectangle PQRS are intersecting in point M. If ∠QMR = 50° find the measure of ∠MPS.
If the diagonals of a parallelogram are of equal lengths, the parallelogram is a rectangle. Prove it.
ABCD is a rectangle whose diagonals AC and BD intersect at O. If ∠OAB = 46°, find ∠OBC
Show that the bisectors of angles of a parallelogram form a rectangle
A parallelogram PQRS is constructed with sides QR = 6 cm, PQ = 4 cm and ∠PQR = 90°. Then PQRS is a ______.
A line l is parallel to line m and a transversal p intersects them at X, Y respectively. Bisectors of interior angles at X and Y interesct at P and Q. Is PXQY a rectangle? Given reason.
