Advertisements
Advertisements
प्रश्न
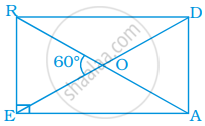
ABCD is a rectangle whose diagonals AC and BD intersect at O. If ∠OAB = 46°, find ∠OBC
उत्तर
Since the diagonals of a rectangle AC and BD are equal and bisect each other
∴ OA = OB
∠OAB = ∠OBA = 46°
Each angle of a rectangle measures 90°
∠ABC = 90°
∠ABO + ∠OBC = 90°
46° + ∠OBC = 90°
∠OBC = 90° − 46°
∴ ∠OBC = 44°
APPEARS IN
संबंधित प्रश्न
ABC is a right-angled triangle and O is the mid point of the side opposite to the right angle. Explain why O is equidistant from A, B and C. (The dotted lines are drawn additionally to help you)
Which of the following statement is true for a rectangle?
Its diagonals are perpendicular and bisect each other.
Fill in the blank in the following, so as to make the statement true:
A rectangle is a parallelogram in which .....
In a rectangle ABCD, prove that ∆ACB ≅ ∆CAD.
Diagonals of a rectangle PQRS are intersecting in point M. If ∠QMR = 50° find the measure of ∠MPS.
The following figure is a rectangle in which x: y = 3: 7; find the values of x and y.
Show that the bisectors of angles of a parallelogram form a rectangle
Rectangle is a regular quadrilateral.
If diagonals of a quadrilateral are equal, it must be a rectangle.
In rectangle READ, find ∠EAR, ∠RAD and ∠ROD