Advertisements
Advertisements
Question
ABCD is a rectangle whose diagonals AC and BD intersect at O. If ∠OAB = 46°, find ∠OBC
Solution
Since the diagonals of a rectangle AC and BD are equal and bisect each other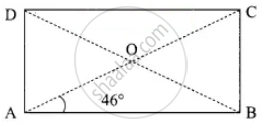
∴ OA = OB
∠OAB = ∠OBA = 46°
Each angle of a rectangle measures 90°
∠ABC = 90°
∠ABO + ∠OBC = 90°
46° + ∠OBC = 90°
∠OBC = 90° − 46°
∴ ∠OBC = 44°
APPEARS IN
RELATED QUESTIONS
Two adjacent angles of a parallelogram are (3x − 4)° and (3x + 10)°. Find the angles of the parallelogram.
Fill in the blank in the following, so as to make the statement true:
A square is a rhombus in which .....
The sides of a rectangle are in the ratio 4 : 5. Find its sides if the perimeter is 90 cm.
A mason has made a concrete slab. He needs it to be rectangular. In what different ways can he make sure that it is rectangular?
Draw a rectangle ABCD such that l(AB) = 6.0 cm and l (BC) = 4.5 cm.
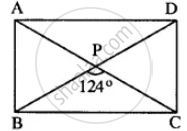
ABCD is a rectangle, if ∠BPC = 124°
Calculate:
- ∠BAP
- ∠ADP
The following figure is a rectangle in which x: y = 3: 7; find the values of x and y.
Show that the bisectors of angles of a parallelogram form a rectangle
A parallelogram PQRS is constructed with sides QR = 6 cm, PQ = 4 cm and ∠PQR = 90°. Then PQRS is a ______.
Construct a rectangle whose one side is 3 cm and a diagonal equal to 5 cm.
