Advertisements
Advertisements
Question
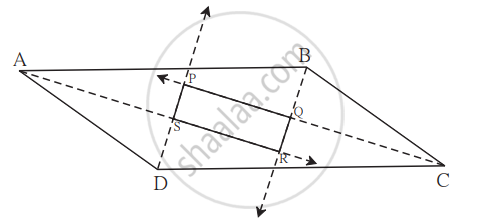
Show that the bisectors of angles of a parallelogram form a rectangle
Solution
Given: A parallelogram in which bisector of angle A, B, C, D intersect at P, Q, R, S to form a quadrilateral PQRS.
To prove: Quadrilateral PQRS is a rectangle.
Proof: Since ABCD is a parallelogram.
Therefore, AB || DC.
Now, AB || DC, and transversal AD cuts them, so we have
∠A + ∠D = 180°
`1/2 ∠"A" + 1/2 ∠ "D" = (180^circ)/2`
∠DAS + ∠ADS = 90°
But in ΔASD, we have
∠ADS + ∠DAS + ∠ASD = 180°
90° + ∠ASD = 180°
∠ASD = 90°
∠RSP = ∠ASD ...(vertically opposite angle)
∠RSP = 90°
Similarly, we can prove that
∠SRQ = 90°, ∠RQP = 90° and ∠QPS = 90°
Thus, PQRS is a quadrilateral each of whose angle is 90°.
Hence, PQRS is a rectangle.
APPEARS IN
RELATED QUESTIONS
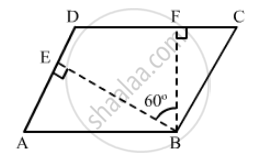
The angle between the altitudes of a parallelogram, through the same vertex of an obtuse angle of the parallelogram is 60°. Find the angles of the parallelogram.
In Fig. 17.29, suppose it is known that DE = DF. Then, is ΔABC isosceles? Why or why not?
A window frame has one diagonal longer than the other. Is the window frame a rectangle? Why or why not?
Prove that quadrilateral formed by the intersection of angle bisectors of all angles of a parallelogram is a rectangle.
State with reason whether the following statement is ‘true’ or ‘false’.
Every parallelogram is a rectangle.
The following figure is a rectangle in which x: y = 3: 7; find the values of x and y.
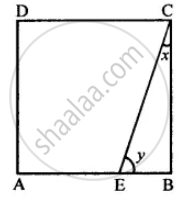
For which of the following figures, diagonals are equal?
If the adjacent angles of a parallelogram are equal, then the parallelogram is a ______.
Rectangle is a regular quadrilateral.
Quadrilateral EFGH is a rectangle in which J is the point of intersection of the diagonals. Find the value of x if JF = 8x + 4 and EG = 24x – 8.
