Advertisements
Advertisements
प्रश्न
Show that the bisectors of angles of a parallelogram form a rectangle
उत्तर
Given: A parallelogram in which bisector of angle A, B, C, D intersect at P, Q, R, S to form a quadrilateral PQRS.
To prove: Quadrilateral PQRS is a rectangle.
Proof: Since ABCD is a parallelogram.
Therefore, AB || DC.
Now, AB || DC, and transversal AD cuts them, so we have
∠A + ∠D = 180°
`1/2 ∠"A" + 1/2 ∠ "D" = (180^circ)/2`
∠DAS + ∠ADS = 90°
But in ΔASD, we have
∠ADS + ∠DAS + ∠ASD = 180°
90° + ∠ASD = 180°
∠ASD = 90°
∠RSP = ∠ASD ...(vertically opposite angle)
∠RSP = 90°
Similarly, we can prove that
∠SRQ = 90°, ∠RQP = 90° and ∠QPS = 90°
Thus, PQRS is a quadrilateral each of whose angle is 90°.
Hence, PQRS is a rectangle.
APPEARS IN
संबंधित प्रश्न
Name the quadrilaterals whose diagonals are equal
In a parallelogram ABCD, the diagonals bisect each other at O. If ∠ABC = 30°, ∠BDC = 10° and ∠CAB = 70°. Find:
∠DAB, ∠ADC, ∠BCD, ∠AOD, ∠DOC, ∠BOC, ∠AOB, ∠ACD, ∠CAB, ∠ADB, ∠ACB, ∠DBC and ∠DBA.
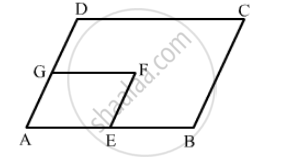
In the following figure, ABCD and AEFG are parallelograms. If ∠C = 55°, what is the measure of ∠F?
Which of the following statement is true for a rectangle?
Its diagonals are equal.
Draw a rectangle whose one side measures 8 cm and the length of each of whose diagonals is 10 cm.
A mason has made a concrete slab. He needs it to be rectangular. In what different ways can he make sure that it is rectangular?
Using opposite angles test for parallelogram, prove that every rectangle is a parallelogram.
State with reason whether the following statement is ‘true’ or ‘false’.
Every parallelogram is a rectangle.
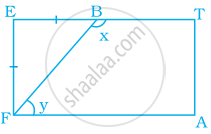
A playground is in the form of a rectangle ATEF. Two players are standing at the points F and B where EF = EB. Find the values of x and y.
Quadrilateral EFGH is a rectangle in which J is the point of intersection of the diagonals. Find the value of x if JF = 8x + 4 and EG = 24x – 8.
