Advertisements
Advertisements
प्रश्न
Quadrilateral EFGH is a rectangle in which J is the point of intersection of the diagonals. Find the value of x if JF = 8x + 4 and EG = 24x – 8.
उत्तर
Given, EFGH is a rectangle in which diagonals are intersecting at the point J.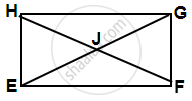
We know that, the diagonals of a rectangle bisect each other and are equal.
Then, EG = 2 × JF
⇒ 24x – 8 = 2(8x + 4)
⇒ 24x – 8 = 16x + 8
⇒ 24x – 16x = 8 + 8
⇒ 8x = 16
⇒ x = 2
APPEARS IN
संबंधित प्रश्न
Which of the following statement is true for a rectangle?
Its diagonals bisect each other.
Which of the following statement is true for a rectangle?
All rectangles are squares.
Which of the following statement true for a square?
Its diagonals bisect each other at right angle.
Draw a rectangle whose one side measures 8 cm and the length of each of whose diagonals is 10 cm.
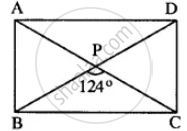
ABCD is a rectangle, if ∠BPC = 124°
Calculate:
- ∠BAP
- ∠ADP
For which of the following figures, diagonals are equal?
If the diagonals of a quadrilateral are equal and bisect each other, then the quadrilateral is a ______.
Every trapezium is a rectangle.
In a rectangle ABCD, AB = 25 cm and BC = 15. In what ratio does the bisector of ∠C divide AB?
A line l is parallel to line m and a transversal p intersects them at X, Y respectively. Bisectors of interior angles at X and Y interesct at P and Q. Is PXQY a rectangle? Given reason.
