Advertisements
Advertisements
प्रश्न
A line l is parallel to line m and a transversal p intersects them at X, Y respectively. Bisectors of interior angles at X and Y interesct at P and Q. Is PXQY a rectangle? Given reason.
उत्तर
Given, l || m
Now, ∠DXY = ∠XYA ...[Alternate interior angles]
⇒ `(∠DXY)/2 = (∠XYA)/2` ...[Dividing both the sides by 2]
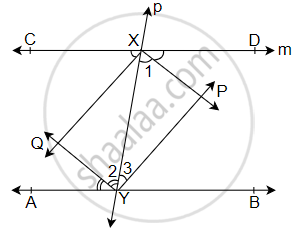
Now, ∠1 = ∠2 ...[Alternate angle are equal]
XP and YQ are bisectors.
So, XP || QY ...(i)
Similarly, XQ || PY ...(ii)
Now, from equation (i) and (ii), we get
In parallelogram PXQY,
∠DXY + ∠XYB = 180° ...(iii) [Interior angles on the same side of transversal are supplementary]
Now, dividing both the sides by 2, get
`(∠DXY)/2 + (∠XYB)/2 = 180^circ/2`
So, ∠1 + ∠3 = 90° [Dividing both the sides by 2] ...(iv)
In triangle XYP,
∠1 + ∠3 + ∠P = 180°
90° + ∠P = 180° ...[From equation (iv)]
∠P = 180° – 90°
∠P = 90° ...(v)
From equations (iii) and (v),
PXQY is a rectangle.
APPEARS IN
संबंधित प्रश्न
In Fig. 17.29, suppose it is known that DE = DF. Then, is ΔABC isosceles? Why or why not?
Which of the following statement is true for a rectangle?
It has two pairs of equal sides.
Which of the following statement is true for a rectangle?
Its diagonals are perpendicular.
Which of the following statement is true for a rectangle?
Its diagonals are perpendicular and bisect each other.
Which of the following statement is true for a square?
It is a rectangle.
Which of the following statement true for a square?
Its diagonals are equal to its sides.
The sides of a rectangle are in the ratio 2 : 3, and its perimeter is 20 cm. Draw the rectangle.
Draw a rectangle whose one side measures 8 cm and the length of each of whose diagonals is 10 cm.
If the diagonals of a quadrilateral are equal and bisect each other, then the quadrilateral is a ______.
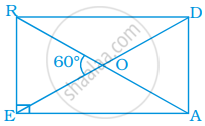
In rectangle READ, find ∠EAR, ∠RAD and ∠ROD