Advertisements
Chapters
2: Data Handling
3: Square-Square Root and Cube-Cube Root
4: Linear Equation In One Variable
▶ 5: Understanding Quadrilaterals and Practical Geometry
6: Visualising Solid Shapes
7: Algebraic Expression, Identities and Factorisation
8: Exponents and Powers
9: Comparing Quantities
10: Direct and Inverse Proportions
11: Mensuration
12: Introduct To Graphs
13: Playing With Numbers
![NCERT Exemplar solutions for Mathematics [English] Class 8 chapter 5 - Understanding Quadrilaterals and Practical Geometry NCERT Exemplar solutions for Mathematics [English] Class 8 chapter 5 - Understanding Quadrilaterals and Practical Geometry - Shaalaa.com](/images/mathematics-english-class-8_6:5f2b1b2038084cf381bfa42c826a928c.jpg)
Advertisements
Solutions for Chapter 5: Understanding Quadrilaterals and Practical Geometry
Below listed, you can find solutions for Chapter 5 of CBSE NCERT Exemplar for Mathematics [English] Class 8.
NCERT Exemplar solutions for Mathematics [English] Class 8 5 Understanding Quadrilaterals and Practical Geometry Exercise [Pages 144 - 163]
Choose the correct alternative:
If three angles of a quadrilateral are each equal to 75°, the fourth angle is ______.
150°
135°
45°
75°
For which of the following, diagonals bisect each other?
Square
Kite
Trapezium
Quadrilateral
For which of the following figures, all angles are equal?
Rectangle
Kite
Trapezium
Rhombus
For which of the following figures, diagonals are perpendicular to each other?
Parallelogram
Kite
Trapezium
Rectangle
For which of the following figures, diagonals are equal?
Trapezium
Rhombus
Parallelogram
Rectangle
Which of the following figures satisfy the following properties?
- All sides are congruent.
- All angles are right angles.
- Opposite sides are parallel.
Which of the following figures satisfy the following property?
- Has two pairs of congruent adjacent sides.
Which of the following figures satisfy the following property?
- Only one pair of sides are parallel.
Which of the following figures do not satisfy any of the following properties?
- All sides are equal.
- All angles are right angles.
- Opposite sides are parallel.
Which of the following properties describe a trapezium?
A pair of opposite sides is parallel.
The diagonals bisect each other.
The diagonals are perpendicular to each other.
The diagonals are equal.
Which of the following is a property of a parallelogram?
Opposite sides are parallel.
The diagonals bisect each other at right angles.
The diagonals are perpendicular to each other.
All angles are equal.
What is the maximum number of obtuse angles that a quadrilateral can have?
1
2
3
4
How many non-overlapping triangles can we make in a n-gon (polygon having n sides), by joining the vertices?
n – 1
n – 2
n – 3
n – 4
What is the sum of all the angles of a pentagon?
180°
360°
540°
720°
What is the sum of all angles of a hexagon?
180°
360°
540°
720°
If two adjacent angles of a parallelogram are (5x – 5)° and (10x + 35)°, then the ratio of these angles is ______.
1 : 3
2 : 3
1 : 4
1 : 2
A quadrilateral whose all sides are equal, opposite angles are equal and the diagonals bisect each other at right angles is a ______.
rhombus
parallelogram
square
rectangle
A quadrilateral whose opposite sides and all the angles are equal is a ______.
rectangle
parallelogram
square
rhombus
A quadrilateral whose all sides, diagonals and angles are equal is a ______.
square
trapezium
rectangle
rhombus
How many diagonals does a hexagon have?
9
8
2
6
If the adjacent sides of a parallelogram are equal then parallelogram is a ______.
rectangle
trapezium
rhombus
square
If the diagonals of a quadrilateral are equal and bisect each other, then the quadrilateral is a ______.
rhombus
rectangle
square
parallelogram
The sum of all exterior angles of a triangle is ______.
180°
360°
540°
720°
Which of the following is an equiangular and equilateral polygon?
Square
Rectangle
Rhombus
Right triangle
Which one has all the properties of a kite and a parallelogram?
Trapezium
Rhombus
Rectangle
Parallelogram
The angles of a quadrilateral are in the ratio 1 : 2 : 3 : 4. The smallest angle is ______.
72°
144°
36°
18°
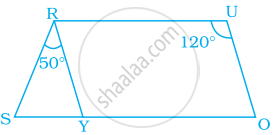
In the trapezium ABCD, the measure of ∠D is ______.
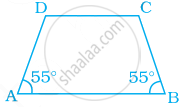
55°
115°
135°
125°
A quadrilateral has three acute angles. If each measures 80°, then the measure of the fourth angle is ______.
150°
120°
105°
140°
The number of sides of a regular polygon where each exterior angle has a measure of 45° is ______.
8
10
4
6
In a parallelogram PQRS, if ∠P = 60°, then other three angles are ______.
45°, 135°, 120°
60°, 120°, 120°
60°, 135°, 135°
45°, 135°, 135°
If two adjacent angles of a parallelogram are in the ratio 2 : 3, then the measure of angles are ______.
72°, 108°
36°, 54°
80°, 120°
96°, 144°
If PQRS is a parallelogram, then ∠P – ∠R is equal to ______.
60°
90°
80°
0°
The sum of adjacent angles of a parallelogram is ______.
180°
120°
360°
90°
The angle between the two altitudes of a parallelogram through the same vertex of an obtuse angle of the parallelogram is 30°. The measure of the obtuse angle is ______.
100°
150°
105°
120°
In the given figure, ABCD and BDCE are parallelograms with common base DC. If BC ⊥ BD, then ∠BEC = ______.
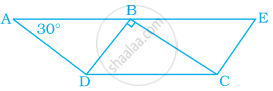
60°
30°
150°
120°
Length of one of the diagonals of a rectangle whose sides are 10 cm and 24 cm is ______.
25 cm
20 cm
26 cm
3.5 cm
If the adjacent angles of a parallelogram are equal, then the parallelogram is a ______.
rectangle
trapezium
rhombus
any of the three
Which of the following can be four interior angles of a quadrilateral?
140°, 40°, 20°, 160°
270°, 150°, 30°, 20°
40°, 70°, 90°, 60°
110°, 40°, 30°, 180°
The sum of angles of a concave quadrilateral is ______.
more than 360°
less than 360°
equal to 360°
twice of 360°
Which of the following can never be the measure of exterior angle of a regular polygon?
22°
36°
45°
30°
In the figure, BEST is a rhombus, Then the value of y – x is ______.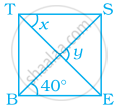
40°
50°
20°
10°
The closed curve which is also a polygon is ______.
Which of the following is not true for an exterior angle of a regular polygon with n sides?
Each exterior angle = `360^circ/n`
Exterior angle = 180° – interior angle
`n = 360^circ/"exterior angle"`
Each exterior angle = `((n - 2) xx 180^circ)/n`
PQRS is a square. PR and SQ intersect at O. Then ∠POQ is a ______.
Right angle
Straight angle
Reflex angle
Complete angle
Two adjacent angles of a parallelogram are in the ratio 1:5. Then all the angles of the parallelogram are ______.
30°, 150°, 30°, 150°
85°, 95°, 85°, 95°
45°, 135°, 45°, 135°
30°, 180°, 30°, 180°
A parallelogram PQRS is constructed with sides QR = 6 cm, PQ = 4 cm and ∠PQR = 90°. Then PQRS is a ______.
square
rectangle
rhombus
trapezium
The angles P, Q, R and S of a quadrilateral are in the ratio 1:3:7:9. Then PQRS is a ______.
parallelogram
trapezium with PQ || RS
trapezium with QR || PS
kite
PQRS is a trapezium in which PQ || SR and ∠P = 130°, ∠Q = 110°. Then ∠R is equal to ______.
70°
50°
65°
55°
The number of sides of a regular polygon whose each interior angle is of 135° is ______.
6
7
8
9
If a diagonal of a quadrilateral bisects both the angles, then it is a ______.
kite
parallelogram
rhombus
rectangle
To construct a unique parallelogram, the minimum number of measurements required is ______.
2
3
4
5
To construct a unique rectangle, the minimum number of measurements required is ______.
4
3
2
1
Fill in the blanks:
In quadrilateral HOPE, the pairs of opposite sides are ______.
In quadrilateral ROPE, the pairs of adjacent angles are ______.
In quadrilateral WXYZ, the pairs of opposite angles are ______.
The diagonals of the quadrilateral DEFG are ______ and ______.
The sum of all ______ of a quadrilateral is 360°.
The measure of each exterior angle of a regular pentagon is ______.
Sum of the angles of a hexagon is ______.
The measure of each exterior angle of a regular polygon of 18 sides is ______.
The number of sides of a regular polygon, where each exterior angle has a measure of 36°, is ______.
 is a closed curve entirely made up of line segments. The another name for this shape is ______.
is a closed curve entirely made up of line segments. The another name for this shape is ______.
A quadrilateral that is not a parallelogram but has exactly two opposite angles of equal measure is ______.
The measure of each angle of a regular pentagon is ______.
The name of three-sided regular polygon is ______.
The number of diagonals in a hexagon is ______.
A polygon is a simple closed curve made up of only ______.
A regular polygon is a polygon whose all sides are equal and all ______ are equal.
The sum of interior angles of a polygon of n sides is ______ right angles.
The sum of all exterior angles of a polygon is ______.
______ is a regular quadrilateral.
A quadrilateral in which a pair of opposite sides is parallel is ______.
If all sides of a quadrilateral are equal, it is a ______.
In a rhombus diagonals intersect at ______ angles.
______ measurements can determine a quadrilateral uniquely.
A quadrilateral can be constructed uniquely if its three sides and ______ angles are given.
A rhombus is a parallelogram in which ______ sides are equal.
The measure of ______ angle of concave quadrilateral is more than 180°.
A diagonal of a quadrilateral is a line segment that joins two ______ vertices of the quadrilateral.
The number of sides in a regular polygon having measure of an exterior angle as 72° is ______.
If the diagonals of a quadrilateral bisect each other, it is a ______.
The adjacent sides of a parallelogram are 5 cm and 9 cm. Its perimeter is ______.
A nonagon has ______ sides.
Diagonals of a rectangle are ______.
A polygon having 10 sides is known as ______.
A rectangle whose adjacent sides are equal becomes a ______.
If one diagonal of a rectangle is 6 cm long, length of the other diagonal is ______.
Adjacent angles of a parallelogram are ______.
If only one diagonal of a quadrilateral bisects the other, then the quadrilateral is known as ______.
In trapezium ABCD with AB || CD, if ∠A = 100°, then ∠D = ______.
The polygon in which sum of all exterior angles is equal to the sum of interior angles is called ______.
State whether the following statement is True or False:
All angles of a trapezium are equal.
True
False
All squares are rectangles.
True
False
All kites are squares.
True
False
All rectangles are parallelograms.
True
False
All rhombuses are squares.
True
False
Sum of all the angles of a quadrilateral is 180°.
True
False
A quadrilateral has two diagonals.
True
False
Triangle is a polygon whose sum of exterior angles is double the sum of interior angles.
True
False
 is a polygon.
is a polygon.
True
False
A kite is not a convex quadrilateral.
True
False
The sum of interior angles and the sum of exterior angles taken in an order are equal in case of quadrilaterals only.
True
False
If the sum of interior angles is double the sum of exterior angles taken in an order of a polygon, then it is a hexagon.
True
False
A polygon is regular if all of its sides are equal.
True
False
Rectangle is a regular quadrilateral.
True
False
If diagonals of a quadrilateral are equal, it must be a rectangle.
True
False
If opposite angles of a quadrilateral are equal, it must be a parallelogram.
True
False
The interior angles of a triangle are in the ratio 1:2:3, then the ratio of its exterior angles is 3:2:1.
True
False
 is a concave pentagon.
is a concave pentagon.
True
False
Diagonals of a rhombus are equal and perpendicular to each other.
True
False
Diagonals of a rectangle are equal.
True
False
Diagonals of rectangle bisect each other at right angles.
True
False
Every kite is a parallelogram.
True
False
Every trapezium is a parallelogram.
True
False
Every parallelogram is a rectangle.
True
False
Every trapezium is a rectangle.
True
False
Every rectangle is a trapezium.
True
False
Every square is a rhombus.
True
False
Every square is a parallelogram.
True
False
Every square is a trapezium.
True
False
Every rhombus is a trapezium.
True
False
A quadrilateral can be drawn if only measures of four sides are given.
True
False
A quadrilateral can have all four angles as obtuse.
True
False
A quadrilateral can be drawn if all four sides and one diagonal is known.
True
False
A quadrilateral can be drawn when all the four angles and one side is given.
True
False
A quadrilateral can be drawn if all four sides and one angle is known.
True
False
A quadrilateral can be drawn if three sides and two diagonals are given.
True
False
If diagonals of a quadrilateral bisect each other, it must be a parallelogram.
True
False
A quadrilateral can be constructed uniquely if three angles and any two sides are given.
True
False
A parallelogram can be constructed uniquely if both diagonals and the angle between them is given.
True
False
A rhombus can be constructed uniquely if both diagonals are given.
True
False
Solve the following:
The diagonals of a rhombus are 8 cm and 15 cm. Find its side.
Two adjacent angles of a parallelogram are in the ratio 1:3. Find its angles.
Of the four quadrilaterals-square, rectangle, rhombus and trapezium-one is somewhat different from the others because of its design. Find it and give justification.
In a rectangle ABCD, AB = 25 cm and BC = 15. In what ratio does the bisector of ∠C divide AB?
PQRS is a rectangle. The perpendicular ST from S on PR divides ∠S in the ratio 2:3. Find ∠TPQ.
A photo frame is in the shape of a quadrilateral. With one diagonal longer than the other. Is it a rectangle? Why or why not?
The adjacent angles of a parallelogram are (2x – 4)° and (3x – 1)°. Find the measures of all angles of the parallelogram.
The point of intersection of diagonals of a quadrilateral divides one diagonal in the ratio 1:2. Can it be a parallelogram? Why or why not?
The ratio between exterior angle and interior angle of a regular polygon is 1:5. Find the number of sides of the polygon.
Two sticks each of length 5 cm are crossing each other such that they bisect each other. What shape is formed by joining their endpoints? Give reason.
Two sticks each of length 7 cm are crossing each other such that they bisect each other at right angles. What shape is formed by joining their end points? Give reason.
A playground in the town is in the form of a kite. The perimeter is 106 metres. If one of its sides is 23 metres, what are the lengths of other three sides?
In rectangle READ, find ∠EAR, ∠RAD and ∠ROD
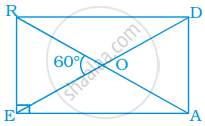
In rectangle PAIR, find ∠ARI, ∠RMI and ∠PMA.
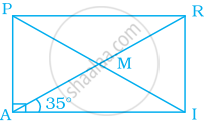
In parallelogram ABCD, find ∠B, ∠C and ∠D.

In parallelogram PQRS, O is the mid point of SQ. Find ∠S, ∠R, PQ, QR and diagonal PR.
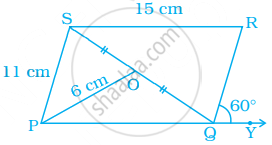
In rhombus BEAM, find ∠AME and ∠AEM.
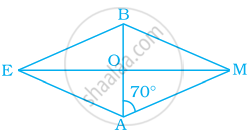
In parallelogram FIST, find ∠SFT, ∠OST and ∠STO.
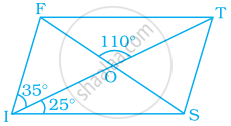
In the given parallelogram YOUR, ∠RUO = 120° and OY is extended to point S such that ∠SRY = 50°. Find ∠YSR.
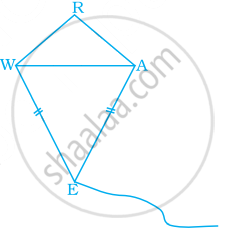
In kite WEAR, ∠WEA = 70° and ∠ARW = 80°. Find the remaining two angles.
A rectangular MORE is shown below:
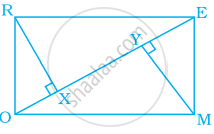
Answer the following questions by giving appropriate reason.
- Is RE = OM?
- Is ∠MYO = ∠RXE?
- Is ∠MOY = ∠REX?
- Is ΔMYO ≅ ΔRXE?
- Is MY = RX?
In parallelogram LOST, SN ⊥ OL and SM ⊥ LT. Find ∠STM, ∠SON and ∠NSM.

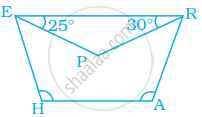
In trapezium HARE, EP and RP are bisectors of ∠E and ∠R respectively. Find ∠HAR and ∠EHA.
In parallelogram MODE, the bisector of ∠M and ∠O meet at Q, find the measure of ∠MQO.
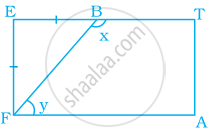
A playground is in the form of a rectangle ATEF. Two players are standing at the points F and B where EF = EB. Find the values of x and y.
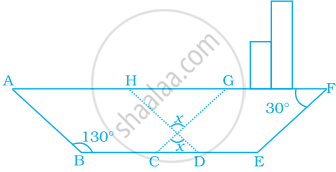
In the following figure of a ship, ABDH and CEFG are two parallelograms. Find the value of x.
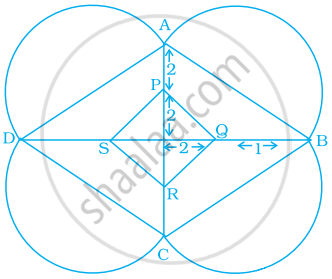
A Rangoli has been drawn on a flor of a house. ABCD and PQRS both are in the shape of a rhombus. Find the radius of semicircle drawn on each side of rhombus ABCD.
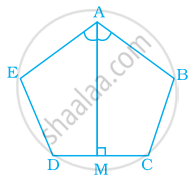
ABCDE is a regular pentagon. The bisector of angle A meets the side CD at M. Find ∠AMC.
Quadrilateral EFGH is a rectangle in which J is the point of intersection of the diagonals. Find the value of x if JF = 8x + 4 and EG = 24x – 8.
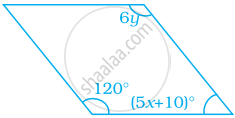
Find the values of x and y in the following parallelogram.
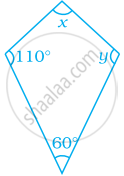
Find the values of x and y in the following kite.
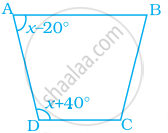
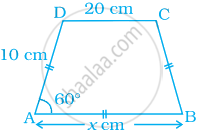
Find the value of x in the trapezium ABCD given below.
Two angles of a quadrilateral are each of measure 75° and the other two angles are equal. What is the measure of these two angles? Name the possible figures so formed.
In a quadrilateral PQRS, ∠P = 50°, ∠Q = 50°, ∠R = 60°. Find ∠S. Is this quadrilateral convex or concave?
Both the pairs of opposite angles of a quadrilateral are equal and supplementary. Find the measure of each angle.
Find the measure of each angle of a regular octagon.
Find the measure of an are exterior angle of a regular pentagon and an exterior angle of a regular decagon. What is the ratio between these two angles?
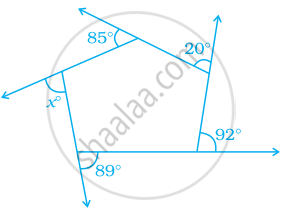
In the figure, find the value of x.
Three angles of a quadrilateral are equal. Fourth angle is of measure 120°. What is the measure of equal angles?
In a quadrilateral HOPE, PS and ES are bisectors of ∠P and ∠E respectively. Give reason.
ABCD is a parallelogram. Find the value of x, y and z.

Diagonals of a quadrilateral are perpendicular to each other. Is such a quadrilateral always a rhombus? Give a figure to justify your answer.
ABCD is a trapezium such that AB || CD, ∠A : ∠D = 2 : 1, ∠B : ∠C = 7 : 5. Find the angles of the trapezium.
A line l is parallel to line m and a transversal p intersects them at X, Y respectively. Bisectors of interior angles at X and Y interesct at P and Q. Is PXQY a rectangle? Given reason.
ABCD is a parallelogram. The bisector of angle A intersects CD at X and bisector of angle C intersects AB at Y. Is AXCY a parallelogram? Give reason.
A diagonal of a parallelogram bisects an angle. Will it also bisect the other angle? Give reason.
The angle between the two altitudes of a parallelogram through the vertex of an obtuse angle of the parallelogram is 45°. Find the angles of the parallelogram.
ABCD is a rhombus such that the perpendicular bisector of AB passes through D. Find the angles of the rhombus.
Hint: Join BD. Then ∆ABD is equilateral.
ABCD is a parallelogram. Points P and Q are taken on the sides AB and AD respectively and the parallelogram PRQA is formed. If ∠C = 45°, find ∠R.
In parallelogram ABCD, the angle bisector of ∠A bisects BC. Will angle bisector of B also bisect AD? Give reason.
A regular pentagon ABCDE and a square ABFG are formed on opposite sides of AB. Find ∠BCF.
Find maximum number of acute angles which a convex, a quadrilateral, a pentagon and a hexagon can have. Observe the pattern and generalise the result for any polygon.
In the following figure, FD || BC || AE and AC || ED. Find the value of x.
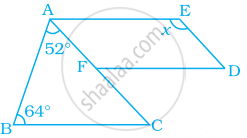
In the following figure, AB || DC and AD = BC. Find the value of x.
Construct a trapezium ABCD in which AB || DC, ∠A = 105°, AD = 3 cm, AB = 4 cm and CD = 8 cm.
Construct a parallelogram ABCD in which AB = 4 cm, BC = 5 cm and ∠B = 60°.
Construct a rhombus whose side is 5 cm and one angle is of 60°.
Construct a rectangle whose one side is 3 cm and a diagonal equal to 5 cm.
Construct a square of side 4 cm.
Construct a rhombus CLUE in which CL = 7.5 cm and LE = 6 cm.
Construct a quadrilateral BEAR in which BE = 6 cm, EA = 7 cm, RB = RE = 5 cm and BA = 9 cm. Measure its fourth side.
Construct a parallelogram POUR in which, PO = 5.5 cm, OU = 7.2 cm and ∠O = 70°.
Draw a circle of radius 3 cm and draw its diameter and label it as AC. Construct its perpendicular bisector and let it intersect the circle at B and D. What type of quadrilateral is ABCD? Justify your answer.
Construct a parallelogram HOME with HO = 6 cm, HE = 4 cm and OE = 3 cm.
Is it possible to construct a quadrilateral ABCD in which AB = 3 cm, BC = 4 cm, CD = 5.4 cm, DA = 5.9 cm and diagonal AC = 8 cm? If not, why?
Is it possible to construct a quadrilateral ROAM in which RO = 4 cm, OA = 5 cm, ∠O = 120°, ∠R = 105° and ∠A = 135°? If not, why?
Construct a square in which each diagonal is 5 cm long.
Construct a quadrilateral NEWS in which NE = 7 cm, EW = 6 cm, ∠N = 60°, ∠E = 110° and ∠S = 85°.
Construct a parallelogram when one of its side is 4 cm and its two diagonals are 5.6 cm and 7 cm. Measure the other side.
Find the measure of each angle of a regular polygon of 20 sides?
Construct a trapezium RISK in which RI || KS, RI = 7 cm, IS = 5 cm, RK = 6.5 cm and ∠I = 60°.
Construct a trapezium ABCD where AB || CD, AD = BC = 3.2 cm, AB = 6.4 cm and CD = 9.6 cm. Measure ∠B and ∠A.
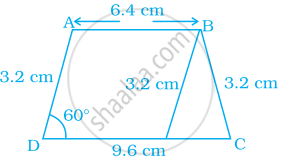
[Hint: Difference of two parallel sides gives an equilateral triangle.]
Solutions for 5: Understanding Quadrilaterals and Practical Geometry
![NCERT Exemplar solutions for Mathematics [English] Class 8 chapter 5 - Understanding Quadrilaterals and Practical Geometry NCERT Exemplar solutions for Mathematics [English] Class 8 chapter 5 - Understanding Quadrilaterals and Practical Geometry - Shaalaa.com](/images/mathematics-english-class-8_6:5f2b1b2038084cf381bfa42c826a928c.jpg)
NCERT Exemplar solutions for Mathematics [English] Class 8 chapter 5 - Understanding Quadrilaterals and Practical Geometry
Shaalaa.com has the CBSE Mathematics Mathematics [English] Class 8 CBSE solutions in a manner that help students grasp basic concepts better and faster. The detailed, step-by-step solutions will help you understand the concepts better and clarify any confusion. NCERT Exemplar solutions for Mathematics Mathematics [English] Class 8 CBSE 5 (Understanding Quadrilaterals and Practical Geometry) include all questions with answers and detailed explanations. This will clear students' doubts about questions and improve their application skills while preparing for board exams.
Further, we at Shaalaa.com provide such solutions so students can prepare for written exams. NCERT Exemplar textbook solutions can be a core help for self-study and provide excellent self-help guidance for students.
Concepts covered in Mathematics [English] Class 8 chapter 5 Understanding Quadrilaterals and Practical Geometry are Properties of Trapezium, Properties of Kite, Classification of Polygons, Properties of a Parallelogram, Concept of Curves, Interior Angles of a Polygon, Exterior Angles of a Polygon and Its Property, Concept of Polygons, Concept of Quadrilaterals, Property: The diagonals of a rhombus are perpendicular bisectors of one another., Properties of Rhombus, Property: The Opposite Sides of a Parallelogram Are of Equal Length., Property: The Opposite Angles of a Parallelogram Are of Equal Measure., Property: The adjacent angles in a parallelogram are supplementary., Property: The diagonals of a parallelogram bisect each other. (at the point of their intersection), Property: The Diagonals of a Rectangle Are of Equal Length., Properties of Rectangle, Properties of a Square, Property: The diagonals of a square are perpendicular bisectors of each other., Properties of a Quadrilateral, Different Types of Curves - Closed Curve, Open Curve, Simple Curve., Constructing a Quadrilateral When the Lengths of Four Sides and a Diagonal Are Given, Constructing a Quadrilateral When Two Diagonals and Three Sides Are Given, Constructing a Quadrilateral When Two Adjacent Sides and Three Angles Are Known, Constructing a Quadrilateral When Three Sides and Two Included Angles Are Given, Some Special Cases, Introduction to Geometric Tool.
Using NCERT Exemplar Mathematics [English] Class 8 solutions Understanding Quadrilaterals and Practical Geometry exercise by students is an easy way to prepare for the exams, as they involve solutions arranged chapter-wise and also page-wise. The questions involved in NCERT Exemplar Solutions are essential questions that can be asked in the final exam. Maximum CBSE Mathematics [English] Class 8 students prefer NCERT Exemplar Textbook Solutions to score more in exams.
Get the free view of Chapter 5, Understanding Quadrilaterals and Practical Geometry Mathematics [English] Class 8 additional questions for Mathematics Mathematics [English] Class 8 CBSE, and you can use Shaalaa.com to keep it handy for your exam preparation.