Advertisements
Advertisements
प्रश्न
The angles P, Q, R and S of a quadrilateral are in the ratio 1:3:7:9. Then PQRS is a ______.
विकल्प
parallelogram
trapezium with PQ || RS
trapezium with QR || PS
kite
उत्तर
The angles P, Q, R and S of a quadrilateral are in the ratio 1:3:7:9. Then PQRS is a trapezium with PQ || RS.
Explanation:
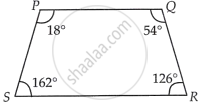
Let the angles be x, 3x, 7x and 9x, then
x + 3x + 7x + 9x = 360° ...[∵ Sum of angles in any quadrilateral is 360°]
⇒ 20x = 360°
⇒ x = `360^circ/20`
⇒ x = 18°
Then, the angles P, Q, R and S are 18°, 54°, 126° and 162°, respectively.
Since, ∠P + ∠S = 18° + 162° = 180° and ∠Q + ∠R = 54° + 126° = 180°
∴ The quadrilateral PQRS is a trapezium with PQ || RS.
APPEARS IN
संबंधित प्रश्न
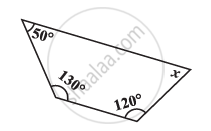
Find the angle measure x in the given Figure
Two opposite angles of a parallelogram are (3x – 2)° and (50 – x)°. Find the measure of each angle of the parallelogram .
If an angle of a parallelogram is two-third of its adjacent angle, find the angles of the parallelogram .
Find the measure of all the angles of a parallelogram, if one angle is 24° less than twice the smallest angle
ABCD is a parallelogram in which ∠A = 70°. Compute ∠B, ∠C and ∠D .
If PQRS is a square, then write the measure of ∠SRP.
If the angles of a quadrilateral are in the ratio 3 : 5 : 9 : 13, then find the measure of the smallest angle.
In a quadrilateral ABCD, bisectors of angles A and B intersect at O such that ∠AOB = 75°, then write the value of ∠C + ∠D.
The angle between two altitudes of a parallelogram through the vertex of an obtuse angle of the parallelogram is 60º. Find the angles of the parallelogram.
In the following figure, P is the mid-point of side BC of a parallelogram ABCD such that ∠BAP = ∠DAP. Prove that AD = 2CD.

