Advertisements
Advertisements
प्रश्न
In the following figure of a ship, ABDH and CEFG are two parallelograms. Find the value of x.
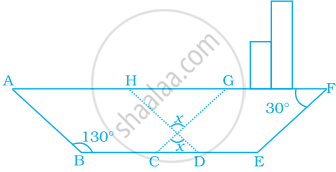
उत्तर
We have, two parallelograms ABDH and CEFG.
Now, In ABDH,
∴ ∠ABD = ∠AHD = 130° ...[∵ Opposite angles of a parallelogram are equal]
And ∠GHD = 180° – ∠AHD
= 180° – 130° ...[Linear pair]
⇒ ∠GHO = 50°
Also, ∠EFG + ∠FGC = 180° ...[∵ Adjacent angles of a parallelogram are supplementary]
⇒ 30° + ∠FGC = 180°
⇒ ∠FGC = 180° – 30° = 150°
And ∠HGC + ∠FGC = 180° ...[Linear pair]
∠HGC = 180° – ∠FGC
= 180° – 150°
∴ ∠HGO = 30°
In ΔHGO, by using angle sum property,
∠OHG + ∠HGO + ∠HOG = 180°
⇒ 50° + 30° + x = 180°
⇒ x = 180° – 80°
= 100°
APPEARS IN
संबंधित प्रश्न
Can a quadrilateral ABCD be a parallelogram if ∠A = 70° and ∠C = 65°?
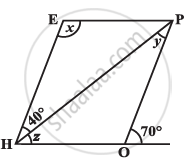
The adjacent figure HOPE is a parallelogram. Find the angle measures x, y and z. State the properties you use to find them.
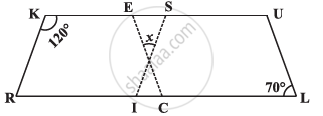
In the above figure both RISK and CLUE are parallelograms. Find the value of x.
If the ratio of measures of two adjacent angles of a parallelogram is 1 : 2, find the measures of all angles of the parallelogram.
In the given figure, if points P, Q, R, S are on the sides of parallelogram such that AP = BQ = CR = DS then prove that `square`PQRS is a parallelogram.

Ratio of consecutive angles of a quadrilateral is 1 : 2 : 3 : 4. Find the measure of its each angle. Write, with reason, what type of a quadrilateral it is.
In parallelogram ABCD, ∠A = 3 times ∠B. Find all the angles of the parallelogram. In the same parallelogram, if AB = 5x – 7 and CD = 3x +1 ; find the length of CD.
Iron rods a, b, c, d, e, and f are making a design in a bridge as shown in the figure. If a || b, c || d, e || f, find the marked angles between c and f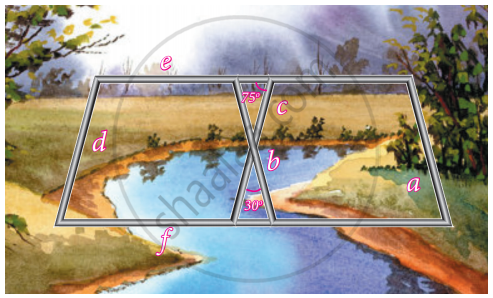
Which of the following is a property of a parallelogram?
The adjacent sides of a parallelogram are 5 cm and 9 cm. Its perimeter is ______.
