Advertisements
Advertisements
Question
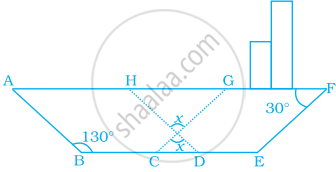
In the following figure of a ship, ABDH and CEFG are two parallelograms. Find the value of x.
Solution
We have, two parallelograms ABDH and CEFG.
Now, In ABDH,
∴ ∠ABD = ∠AHD = 130° ...[∵ Opposite angles of a parallelogram are equal]
And ∠GHD = 180° – ∠AHD
= 180° – 130° ...[Linear pair]
⇒ ∠GHO = 50°
Also, ∠EFG + ∠FGC = 180° ...[∵ Adjacent angles of a parallelogram are supplementary]
⇒ 30° + ∠FGC = 180°
⇒ ∠FGC = 180° – 30° = 150°
And ∠HGC + ∠FGC = 180° ...[Linear pair]
∠HGC = 180° – ∠FGC
= 180° – 150°
∴ ∠HGO = 30°
In ΔHGO, by using angle sum property,
∠OHG + ∠HGO + ∠HOG = 180°
⇒ 50° + 30° + x = 180°
⇒ x = 180° – 80°
= 100°
APPEARS IN
RELATED QUESTIONS
Consider the given parallelogram. Find the values of the unknowns x, y, z.

In the given figure, AB || EC, AB = AC and AE bisects ∠DAC. Prove that:
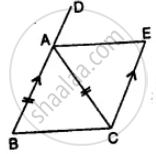
- ∠EAC = ∠ACB
- ABCE is a parallelogram.
Iron rods a, b, c, d, e, and f are making a design in a bridge as shown in the figure. If a || b, c || d, e || f, find the marked angles between b and c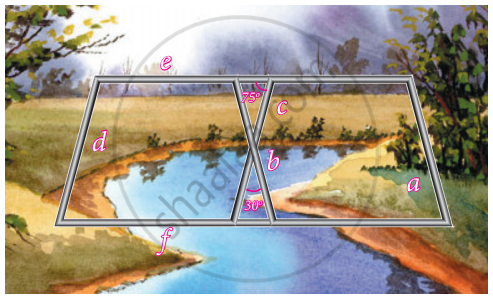
If opposite angles of a quadrilateral are equal, it must be a parallelogram.
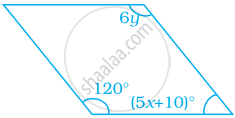
Find the values of x and y in the following parallelogram.
Two angles of a quadrilateral are each of measure 75° and the other two angles are equal. What is the measure of these two angles? Name the possible figures so formed.
ABCD is a parallelogram. Find the value of x, y and z.

ABCD is a parallelogram. Points P and Q are taken on the sides AB and AD respectively and the parallelogram PRQA is formed. If ∠C = 45°, find ∠R.
In parallelogram ABCD, the angle bisector of ∠A bisects BC. Will angle bisector of B also bisect AD? Give reason.
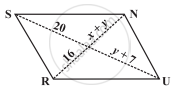
The following figure RUNS is parallelogram. Find x and y. (Lengths are in cm)