Advertisements
Advertisements
Question
In parallelogram ABCD, the angle bisector of ∠A bisects BC. Will angle bisector of B also bisect AD? Give reason.
Solution
Given, ABCD is a parallelogram, bisector of ∠A, bisects BC at F, i.e. ∠1 = ∠2, CF = FB.
Draw FE || BA.
ABFE is a parallelogram by construction ...[∵ FE || BA]
⇒ ∠1 = ∠6 ...[Alternate angle]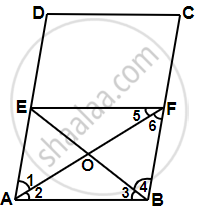
But ∠1 = ∠2 ...[Given]
∴ ∠2 = ∠6
AB = FB [Opposite sides to equal angles are equal] ...(i)
∴ ABFE is a rhombus.
Now, In ΔABO and ΔBOF,
AB = BF ...[From equation (i)]
BO = BO ...[Common]
AO = FO ...[Diagonals of rhombus bisect each other]
∴ ΔABO ≅ ΔBOF ...[By SSS]
∠3 = ∠4 ...[By CPCT]
Now, BF = `1/2` BC ...[Given]
⇒ BF = `1/2` AD ...[BC = AD]
⇒ AE = `1/2` AD ...[BF = AE]
∴ E is the midpoint of AD.
APPEARS IN
RELATED QUESTIONS
Two adjacent angles of a parallelogram have equal measure. Find the measure of each of the angles of the parallelogram.
Name the quadrilaterals whose diagonals bisect each other
Construct a parallelogram ABCD such that l(BC) = 7 cm, m∠ABC = 40° , l(AB) = 3 cm.
In parallelogram ABCD, ∠A = 3 times ∠B. Find all the angles of the parallelogram. In the same parallelogram, if AB = 5x – 7 and CD = 3x +1 ; find the length of CD.
In the following diagram, the bisectors of interior angles of the parallelogram PQRS enclose a quadrilateral ABCD.
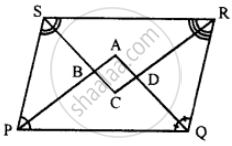
Show that:
(i) ∠PSB + ∠SPB = 90°
(ii) ∠PBS = 90°
(iii) ∠ABC = 90°
(iv) ∠ADC = 90°
(v) ∠A = 90°
(vi) ABCD is a rectangle
Thus, the bisectors of the angles of a parallelogram enclose a rectangle.
In the given figure, AB || EC, AB = AC and AE bisects ∠DAC. Prove that:
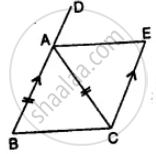
- ∠EAC = ∠ACB
- ABCE is a parallelogram.
Iron rods a, b, c, d, e, and f are making a design in a bridge as shown in the figure. If a || b, c || d, e || f, find the marked angles between d and e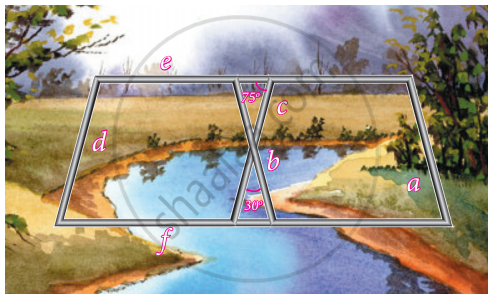
A diagonal of a parallelogram bisects an angle. Will it also bisect the other angle? Give reason.
ABCD is a parallelogram. Points P and Q are taken on the sides AB and AD respectively and the parallelogram PRQA is formed. If ∠C = 45°, find ∠R.
Draw a rough figure of a quadrilateral that is not a parallelogram but has exactly two opposite angles of equal measure.
